Los agujeros negros han atraído la imaginación de científicos y público en general desde que su existencia fue predicha por Karl Schwarzschild en 1919, al encontrarlos como consecuencia de su solución a la teoría general de la relatividad propuesta por Albert Einstein. Estos objetos son devoradores de materia y energía, porque una vez dentro de su frontera llamada horizonte de eventos nada puede escapar de ellos, ni siquiera la luz.
Por eso fue una sorpresa cuando el joven Stephen Hawking publicó en 1974 un artículo de dos páginas en la prestigiosa revista Nature, en el que propuso que los agujeros negros emitían luz, llamada después radiación de Hawking [Hawking1974]. Su derivación incluía efectos de la teoría cuántica, desarrollada en el tiempo intermedio. Hawking propuso una aproximación semi clásica, es decir, la luz se considera un campo cuántico y se estudia en un fondo clásico (no cuántico) de la gravedad del agujero negro. Alguna aproximación es necesaria, porque aun ahora no tenemos una teoría para describir los efectos cuánticos de la gravedad, la hipotética teoría de la “gravedad cuántica”.
Un aspecto importante de la radiación de Hawking es que tiene un espectro térmico, es decir la distribución de frecuencias (color) de la luz emitida, es igual al que emite un cuerpo por tener una temperatura distinta del cero absoluto (esta radiación térmica es la que detectan las cámaras de visión nocturna). Además, el valor de esta temperatura era igual a la predicha por Jacob Bekenstein con consideraciones distintas respecto a la termodinámica de agujeros negros. Por otro lado, la radiación se emite como pares de fotones (o partículas de luz) uno con frecuencia positiva y otro con frecuencia negativa.
Entonces, ¿qué tan real es la radiación de Hawking? Aunque usualmente se considera correcta e incluso se usa como guía para llegar a una teoría de gravedad cuántica [Helfer2003], ésta depende de aspectos no entendidos de la naturaleza como: (i) la dependencia de escalas pequeñas más allá de donde hemos probado nuestras teorías e incluso, más allá de donde creemos que son correctas; (ii) la existencia de luz con frecuencia negativa y (iii) los efectos cuánticos de la gravedad son despreciables en el horizonte de eventos.
William Unruh hizo una propuesta interesante en 1981 para aclarar este efecto [Unruh1981]. Al impartir un curso de mecánica de fluidos, se dio cuenta que las ondas de sonido en un fluido tenían ecuaciones similares a las que llevan a la radiación de Hawking en agujeros negros.
Además, si el fluido tenía velocidad mayor a la velocidad del sonido, entonces el sonido no podían escapar del flujo. Unruh los llamó “agujeros mudos”. El trabajo de Unruh tardó más de una década en tomar relevancia, pero con el tiempo surgió una nueva forma de estudiar la radiación de Hawking como un efecto universal, no restringido al caso astrofísico estudiado originalmente por Hawking. A esta área de estudio se le conoce como “gravedad análoga”.
Los primeros estudios durante la década de los 90s aclararon varios aspectos de la derivación original de Hawking: (i) el efecto no es exclusivo de la interacción de luz con la gravedad y por tanto puede extenderse a otros sistemas de estudio, (ii) el espectro térmico es una propiedad particular del caso astrofísico y en general depende de efectos dispersivos y (iii) las frecuencias negativas deben considerarse reales. A partir del nuevo milenio, varios grupos se enfocaron en la implementación experimental de estos análogos de agujeros negros. Los sistemas más exitosos han sido: ondas superficiales en tanques de agua [Rousseaux2008], ondas de sonido en condensados de Bose-Einstein [Steinhauer2016] y luz en fibras ópticas [Philbin2008]. Pero basta de historia, ahora estudiemos cómo funciona un horizonte de eventos con una analogía acuática.

Imaginemos un río que fluye hacia una cascada tal que la velocidad del agua aumenta en dirección a la cascada, como se muestra en la figura 1. Un pez puede moverse libremente en la zona de flujo lento, lejos de la cascada, sin embargo, hay un punto en que la velocidad del flujo es tal que el pez ya no puede nadar a contracorriente, este es un punto de no retorno. Si cambiamos los peces por ondas, el punto de no retorno se convierte en un análogo del horizonte de eventos para las ondas.
Algo similar sucede para pulsos de luz en fibras ópticas. La velocidad de la luz es constante en el vacío (igual a 300,000 km/s) pero ésta disminuye dentro de un material, lo cual se modela con el llamado índice de refracción, que puede depender de la longitud de onda o el color de la luz.
Además, la energía del pulso mismo cambia un poco el índice de refracción efectivo; el cambio es pequeño, alrededor de mil veces menor que el valor original. Este cambio del índice de refracción se conoce como efecto Kerr y equivale al cambio de la velocidad del flujo del agua en el análogo acuático o al cambio de la gravedad cerca de un agujero negro astrofísico. Si se envía otro pulso de luz puede interactuar con el primer pulso y, si el efecto Hawking fuera cierto, produciría un par de fotones con energías positiva y negativa (como en el caso original estudiado por Hawking).
Este es precisamente el experimento que fue hecho en el laboratorio del Prof. Ulf Leonhardt en el Instituto de Ciencias Weizmann en colaboración con el Cinvestav. A diferencia de experimentos anteriores, en este experimento somos capaces de medir pulsos de luz con frecuencia negativa [Drori2019], además de la frecuencia positiva medida en experimentos previos [Philbin2008].
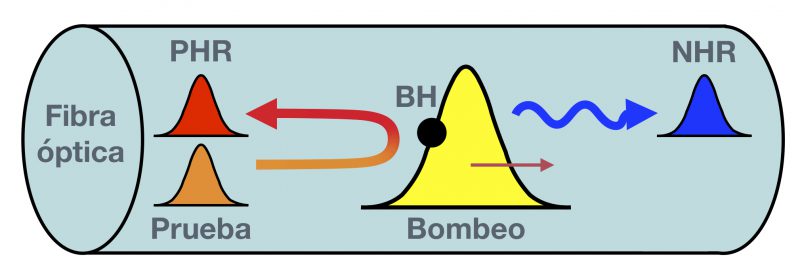
Nuestro experimento consistió en enviar un pulso de luz por una fibra óptica microestructurada de 7 mm de largo, mostrada en la figura 2. Se envía un pulso de bombeo que viene de un láser con longitud de onda de 800nm (nanómetro es 10-9 m, un cabello humano tiene un diámetro de 75,000 nm) de color rojo, intenso y ultra corto; con 7 fs de duración (1 femtosegundo es 10-15 s, esto equivale a 1000 nm de distancia dentro de la fibra). Luego, se envía otro pulso de prueba infrarrojo (1550nm) más débil y más rápido que alcanzará al pulso de bombeo para crear el efecto Hawking. De esta interacción surgen dos señales que son el análogo de la radiación de Hawking: una en el infrarrojo aunque distinguible del original con frecuencia positiva (positive Hawking radiation o PHR, 1580nm) y otra en el ultravioleta (negative Hawking radiation o NHR, 230nm).
Además, hicimos un estudio sistemático de las propiedades de estas señales para asegurarnos que vienen del análogo del efecto Hawking y no de otro efecto óptico dentro de la fibras. Estudiamos su dependencia con la intensidad y la frecuencia de los pulsos originales, obteniendo resultados que se explican con nuestra teoría de análogos. Sin embargo, éste no se considera una prueba final del efecto Hawking, ya que para ello debemos lograr ver el efecto sin la necesidad de usar el segundo pulso, de tal forma que el vacío cuántico mismo estimule la creación del par de fotones en las mismas frecuencias que las medidas en nuestro experimento.
El trabajo experimental fue hecho por un par de estudiantes de doctorado, Jonathan Drori y Yuval Rosenberg, el autor de este texto participó con soluciones numéricas de dinámica de pulsos ultra cortos en fibras ópticas, y Yaron Silberberg y Ulf Leonhardt diseñaron el experimento y supervisaron su realización. Este resultado fue publicado recientemente en Physical Review Letters https:// doi.org/10.1103/PhysRevLett.122.010404 [Drori2019].
Referencias
- Hawking. Black hole explosions, Nature 248 30-31 (1974) https://doi.org/10.1038/248030a0
- Helfer. Do black holes radiate?, Rep. Prog. Phys. 66 943-1008 (2003) https://doi.org/ 10.1088/0034-4885/66/6/202
- Unruh. Experimental black-hole evaporation?, Phys. Rev. Lett. 46 1351-1353 (1981) https://doi.org/10.1103/PhysRevLett.46.1351
- Rousseaux, Mathis, Maissa, Philbin, Leonhardt. Observation of negative-frequency waves in a water tank: a classical analogue to the Hawking effect?, New J. Phys. 10 053015 (2008) https://doi.org/10.1088/1367-2630/10/5/053015
- Steinhauer. Observation of quantum Hawking radiation and its entanglement in an analogue black hole, Nat. Phys. 12 959–965 (2016) https://doi.org/10.1038/nphys3863
- Philbin, Kuklewicz, Robertson, Hill, König, Leonhardt. Fiber-optical analog of the event horizon, Science 319 1367-1370 (2008) https://doi.org/10.1126/science.1153625
- Drori, Rosenberg, Bermudez, Silberberg, Leonhardt. Observation of Stimulated Hawking Radiation in an Optical Analogue, Phys. Rev. Lett. 122 010404 (2019) https://doi.org/10.1103/ PhysRevLett.122.010404
Imagen de portada. Espejo parabólico enfocando los pulsos láser rojo e infrarrojo en la fibra óptica de 7mm. Por su interacción dentro de la fibra se crean dos nuevas frecuencias de luz debido al análogo del efecto Hawking, una en el ultravioleta y otra en el infrarrojo.