Cráteres: de la Luna al laboratorio

Cráteres lunares

En 1609, Galileo Galilei describe detalladamente en su obra Siderius Nuncius (Mensajero Sideral) las observaciones astronómicas que en los dos últimos meses había logrado con el telescopio que acababa de inventar. Hasta ese entonces, se creía que la luna y los cuerpos celestes eran esferas perfectas, lo cual encajaba con la visión religiosa dominante. De sus observaciones lunares, Galileo concluyó:

“…La luna no es lisa ni regular, ni tiene forma exactamente esférica, como ha opinado la turba de filósofos, lo mismo que de otros cuerpos celestes. Todo lo contrario. Es desigual, áspera, con cavidades, con elevaciones, tal cual la tierra en su superficie, que tiene montes y cañadas, valles y depresiones. Y estas son las razones que me da la observación para afirmarlo…”.

Las observaciones de Galileo quedaron plasmadas como la primera evidencia documentada  de depresiones circulares en la superficie lunar, las cuales ahora conocemos como “cráteres”.

 

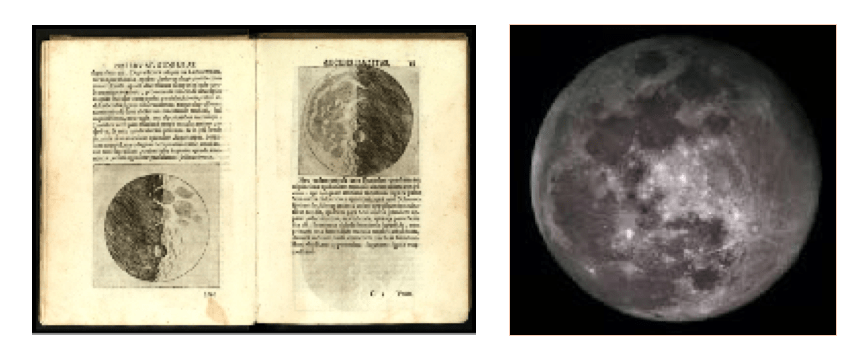
La palabra cráter viene del griego “Krater” que significa “tazón para mezclar” y se acuñó debido a la similitud de las depresiones lunares con la forma de un tazón antiguo que se utilizaba para mezclar vino y agua.

Pero, ¿cuál era el origen de dichas depresiones en la superficie lunar? Galileo no planteó ningún origen, suficientes problemas le causó el describir algo en contra del perfecto mundo sideral de la visión cristiana dominante. Así, tuvieron que pasar varias décadas antes de que Robert Hooke propusiera en 1665 dos mecanismos: erupciones de gas o impactos. A esto se le sumó la actividad volcánica basada en observaciones terrestres. Mientras que una erupción volcánica claramente generaría un cráter, en aquel entonces se consideraba al espacio exterior vacío y la hipótesis de impactos quedó olvidada. Durante más de 200 años la hipótesis del origen volcánico de los cráteres lunares fue dominante. Destacados astrónomos intentaron rescatar la teoría de impacto a inicios del siglo XIX, como el astrónomo alemán Franz Von Paula Gruithuisen, no obstante, unos meses antes publicó que había observado vacas pastando en las praderas lunares y un templo en forma de estrella, lo que le ganó el descrédito de la comunidad astronómica. La hipótesis de impacto retomó nuevamente fuerza a inicios del siglo pasado, cuando Alfred Weneger realizó una revisión exhaustiva de las distintas hipótesis existentes, y notó que reconocidos vulcanólogos, como Johnston-Lavis, habían destacado importantes diferencias entre los cráteres terrestres producidos por erupciones volcánicas y   los cráteres lunares, por lo que descartaban la hipótesis volcánica. Basado en esto, Weneger realizó impactos a escala de laboratorio en el Instituto de Física de Marburg durante dos años (1918-1919). Las morfología de los cráteres obtenidos en sus experimentos reproducían aquellas observadas en la luna: cráteres simples, con picos centrales, terrazas, borde elevados, etc (Weneger1921). Resultados similares se habían observado del impactos de proyectiles en pruebas militares. Por otro lado, estudios geológicos realizados desde 1866 del cráter Barringer (Meteor Crater) en Arizona concluyeron que dicho cráter había sido formado por un meteorito de acero de unos 200 metros de diámetro. Todo apuntaba a que, como el cráter de Arizona, los cráteres lunares habían sido formados por impactos de meteoritos. Trabajos posteriores de Erns Opic, Algernon Glifford, Ralph Baldwing apuntalaron la teoría de impacto, la cual no fue totalmente aceptada sino a finales de los 60’s con la   llegada del hombre a la luna.

 

Cráteres en el laboratorio

Obviamente, el proceso de formación de un cráter por impacto de meteorito no puede estudiarse de manera sistemática a escala natural. Por tal motivo, durante las últimas dos décadas se ha estudiado dicho proceso a escala de laboratorio. En un experimento típico, proyectiles esféricos, sólidos o granulares, se dejan caer desde varias alturas sobre una cama plana de material granular (arena seca o húmeda). Tras la colisión, el material es expulsado desde el punto de impacto formando una cortina uniforme de granos que se dispersa radialmente, mientras se crea una depresión en el suelo que toma la forma final del cráter. Dichos experimentos han demostrado que la morfología de los cráteres resultantes es muy similar a las observada en los cráteres planetarios, lo cual depende de la energía de impacto, del tamaño del grano, del factor de empaquetamiento del medio, entre otros factores (Pacheco2011).

 

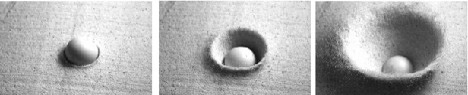
Respecto a las dimensiones del cráter, se ha encontrado que su diámetro, D, escala como una ley de potencias con la energía de impacto, E, con un exponente próximo a 1/4. Dicha dependencia se ha probado válida para un rango de energía de 16 órdenes de magnitud, desde cráteres de unos cuántos centímetros de diámetro formados en una cama de arena, como en la que juegan los niños, hasta cráteres de varios kilómetros observados en las superficies de los planetas. Cuando la energía de impacto es lo suficientemente baja, la vaporización o fusión de la esfera o del material impactado no ocurre. Así, D dependerá de cuatro parámetros independientes: E, la energía perdida por la esfera durante el impacto; d, el diámetro de la esfera; ρ, la densidad del material impactado; y g, la aceleración de la gravedad en la superficie de la Tierra. Este listado de parámetros excluye explícitamente el módulo de resistencia a la fractura del material granular. Tal exclusión implica que el material granular no está consolidado y que los granos pueden separarse sin gasto de energía. Aplicando el Teorema Pi-Buckingham al conjunto de 5 parámetros (D, E, d, ρ, g) y tres dimensiones independientes (longitud, masa, tiempo), se tienen 5-3 = 2 grupos adimensionales que pueden obtenerse por inspección: D/d y E/ ρgd⁴. Entonces D/d= f(E/ ρgd⁴). Puesto que experimentos simples de impacto muestran que D ∝ E^1/4, entonces D ∝(E/ ρg)^1/4 independientemente del diámetro de la esfera. Conforme la energía de impacto aumenta, se reportan pequeñas desviaciones de dicha ley de potencias.

Resumiendo: 1) los cráteres de impacto formados a escala de laboratorio siguen las mismas leyes de escalamiento con la energía que los cráteres a escala planetaria, D ∝ E^1/4. 2) El material es expulsado uniformemente dejando un cráter cuya morfología es similar a la de cráteres lunares. Sin embargo, había un misterio que no había podido ser explicado o reproducido a escala de laboratorio durante las décadas de investigación de estos procesos: los llamados sistemas de rayos.

 

Sistemas de Rayos

Cuando se observa la Luna con un telescopio, como en la Figura 1, se pueden distinguir lineas delgadas saliendo del cráter Tycho. Al conjunto de líneas se le denomina sistemas de rayos, las cuales son eyecciones de material en forma de líneas radiales que salen del punto de impacto y que se extienden considerablemente más allá del diámetro del cráter. Dichas eyecciones pueden o no observarse alrededor de un cráter a escala planetaria, pero no habían sido observadas a escala de laboratorio hasta muy recientemente (Sabuwala2018, Pacheco2019). Durante los últimos seis meses se ha logrado un avance importante en la comprensión del proceso que da origen a los sistemas de rayos. Experimentalmente se demostró por primera vez que existen dos condiciones bajo las cuales se producen sistemas de rayos: a) cuando un proyectil esférico impacta contra una superficie ondulada (Sabuwala2018), o b) cuando un proyectil con curvaturas pronunciadas impacta contra una superficie plana (Pacheco2019). Dichos experimentos tiene gran relevancia considerando que las superficies planetarias no son necesariamente planas y que los meteoritos no son esferas perfectas. Los sistemas de rayos son entonces producidos cuando el material es expulsado en dirección no-radial, ya sea debido a la topología de la superficie o la forma del proyectil, por lo que las eyecciones pueden converger en cierto punto y ser re-dirigidas en un solo rayo.

 

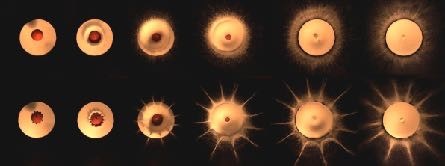
Nos enfocaremos aquí en los sistemas de rayos y cráteres producidos por proyectiles no esféricos, investigación que fue publicada muy recientemente en Physical Review Letters (Pacheco2019). La figura 3 muestra el impacto de dos proyectiles, uno perfectamente esférico y otro con protuberancias. Note que el material expulsado por la esfera forma una cortina uniforme de material, mientras que el material expulsado por el proyectil con 12 protuberancias forma 12 rayos.

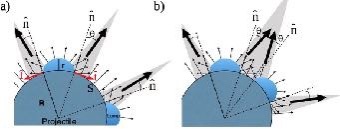
La figura 4a esquematiza un sistema de rayos producidos por el impacto de un proyectil con protuberancias. El diagrama indica cómo el material siempre es expulsado normal a la superficie del proyectil, por lo que la eyección que proviene de una protuberancia colisiona con el material expulsado por la esfera, y al converger, forman un rayo con una ligera desviación respecto a la dirección radial, la cual puede estimarse considerando la conservación del momento lineal. Si dos protuberancias son muy cercanas entre sí, como en el diagrama de la Fig. 4b, dos rayos adyacentes pueden superponerse y generar un rayo de mayor tamaño, por ello, en el caso mostrado en la figura 3, el número de rayos coincide con el número de protuberancias.

 

El lector seguramente cuestionará que un meteorito real no es un proyectil con protuberancias, si no más bien un proyectil amorfo con curvaturas marcadas y/o con pequeñas depresiones. De hecho, la figura 5, tomada de  (Pacheco2019), muestra que un proyectil deforme es capaz de generar un cráter con dos rayos eyectados desde las curvaturas más pronunciadas de su superficie. Esto indica que los sistemas de rayos observados en la luna pudieron haber sido producidos por el impacto de un meteorito con concavidades marcadas, como por ejemplo un meteorito de acero.

 

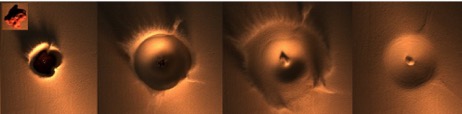
Además, note en la Figura 5 que el cráter resultante tiene una forma circular independientemente de la forma del proyectil. Esto fue corroborado usando proyectiles con distinta geometría de sección transversal y variando la energía de impacto. El cráter final pierde toda la información respecto a la forma del meteorito que lo creó, debido a que la cavidad generada por el impacto se hace más profunda conforme la energía de impacto aumenta. Éste es un resultado de gran relevancia, puesto que explica por qué la mayoría de los cráteres observados en la naturaleza son circulares a pesar de que un meteorito es amorfo.

Las principales aportaciones de la investigación fueron las siguientes (Pacheco2019):

1. Sistemas de rayos pueden producirse por el impacto de un proyectil no esférico que hace converger el material expulsado en una sola dirección, siendo una posible explicación a los enigmáticos sistemas de rayos observados en la Luna.
2. Los cráteres se hacen circulares independientemente de la forma del proyectil conforme la energía de impacto aumenta, lo cual puede explicar porque los cráteres parecen ser circulares aun cuando los meteoritos son de forma irregular.
3. El diámetro del cráter, D, sigue una dependencia con la energía, E, tipo ley de potencias: D∝E^1/4, independientemente de la forma del proyectil (o meteorito).

 

Cráteres producidos por otros mecanismos

Además de los cráteres generados por impacto de meteoritos y erupciones volcánicas, existen cráteres producidos por otros mecanismos, como los cráteres por hundimiento o “maars”. Un maar es producido cuando agua subterránea entra en contacto con el magma y se evapora, el aumento de presión en la cavidad que contiene el gas es capaz de fracturar la capa de rocas; cuando el gas escapa, la superficie se colapsa generando la depresión. Los cráteres también pueden ser producidos de manera artificial mediante explosiones, como el cráter Sedan de 6.5 x 10⁶ m³ creado mediante la explosión de una bomba nuclear de 104 kilotones de TNT en Nevada, el cuál es el cráter más grande creado por el ser humano.

Dichos procesos de formación de cráteres también han sido estudiados a escala de laboratorio por nuestro grupo utilizando materiales granulares, por ejemplo, cráteres producidos mediante explosiones de pequeñas cantidades de pólvora negra en arena (Pacheco2017), colapso de cavidades presurizadas localizadas a distintas profundidades de   un lecho granular (Loranca 2015) y cráteres generados por ablación láser (Marston2019). En el caso de explosiones y ablación láser, el diámetro del cráter escala con la energía liberada como D ∝ E^1/3. Note el exponente 1/3 en vez de 1/4 encontrado para impactos.

 

El análisis mediante perfilometría láser de la geometría de cráteres a escala de laboratorio reveló que cráteres generados por distintos mecanismos tienen distinto perfil: los creados por impacto son parabólicos con borde elevado, los creados por explosiones tienden a ser más hiperbólicos o cónicos, y los creados por colapso de cavidades son depresiones más esféricas sin borde elevado. Así, el análisis de la geometría del cráter nos permite obtener ciertas pistas sobre el posible origen del mismo.

 

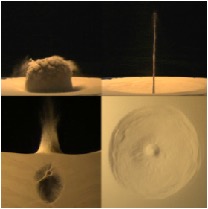
En resumen, el uso de materiales granulares para estudiar formación de cráteres ha sido un método de gran relevancia durante las últimas décadas. Además de dar explicación a los enigmáticos sistemas de rayos.

 

Referencias:

• Weneger1921: A. Weneger Die Entstehung der Mondkrater, Sammlung Vieweg, Heft 55 (1921). Pacheco2011: F. Pacheco-Vázquez and J. C. Ruíz-Suárez, Phys. Rev. Lett 109, 218001 (2011).
• Walsh2003: A. M. Walsh, K. E. Holloway, P. Habdas, and J. R. De Bruyn, Phys. Rev. Lett.91, 104301(2003)
• Loranca2015: F. E. Loranca, J. Carrillo, F. Pacheco-Vázquez Phys. Rev. Lett 115, 028001 (2015).
• Pacheco2017:    F. Pacheco-Vázquez, A. Tacumá and J.O. Marston, Phys. Rev. E 96, 032904 (2017).
• Sabuwala2018: T. Sabuwala, et. al Phys. Rev. Lett. 120, 264501 (2018) Pacheco2019: F. Pacheco-Vázquez, Phys. Rev. Lett. 122, 164501 (2019)
• Marston2019: J.O. Marston and F. Pacheco-Vázquez, Phys. Rev. E 99 030901(R) 2019.