¿Cuál es la transformación relativista de la temperatura bajo cambios de sistemas inerciales?
La teoría de la relatividad tuvo un impacto muy fuerte tanto en la ciencia como en la sociedad. Dos de sus efectos más conocidos fueron la dilatación del tiempo y la contracción del espacio. En 1907 y 1908, un poco después de la aparición de la teoría de la relatividad especial, y prácticamente al mismo tiempo, Planck [1] y Einstein [2] se preguntaron de cuál sería la transformación de la temperatura bajo un cambio de sistema inercial con velocidad relativa relativista. Llegaron al mismo resultado y se describe de la siguiente manera:
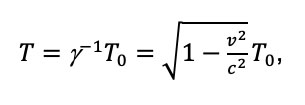
donde T0 representa a la temperatura del cuerpo medido en el sistema de referencia inercial en el cual el cuerpo se encuentra en reposo, T representa la temperatura del cuerpo medido en un sistema en donde está el observador con una velocidad relativa al cuerpo v, y c es la velocidad de la luz. Esto implica que un cuerpo en movimiento con respecto a un observador se ve más frío de lo que está en su sistema en reposo. Otro resultado encontrado con respecto a la transformación del calor fue:
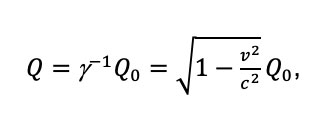
donde el subíndice “0” denota lo mismo que anteriormente. A partir de estas transformaciones se dedujeron todas las demás de las cantidades termodinámicas y se introdujeron los conceptos en la física estadística [3]. Se obtuvo también la equivalente distribución relativista de Boltzmann llamada distribución de Jüttner [4], que contempla la transformación de la temperatura. Sin embargo, aunque todo parecía una teoría acabada, al final de su vida Einstein le comunicó por correspondencia a von Laue [5] sus dudas sobre la validez de las transformaciones relativistas en termodinámica. Al publicar von Laue su correspondencia con Einstein dio lugar a un sinnúmero de nuevas propuestas de las transformaciones relativistas de las cantidades termodinámicas y a una serie de discusiones científicas a lo largo de la segunda mitad del siglo XX. En estas deliberaciones participaron científicos sobresalientes como Tolman, Pauli, Ott, Rohrlich y Landsberg. A finales de los años setenta, Balescu [6] realizó una recopilación de todos los trabajos importantes reviviendo los debates. El tema era fundamental en astrofísica y física de plasmas, pues los choques de jets de partículas a velocidades relativistas eran de gran interés.
Al final se desecharon muchos modelos y se concretaron tres propuestas bastante congruentes [7]. Se resumen de la siguiente manera: la temperatura y el calor se transforman según
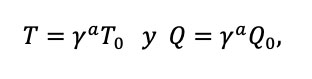
donde a = 1 para la teoría de Ott, a = 0 para la teoría de Landsberg y a = -1 para la teoría de Einstein-Planck. En realidad fue Rohrlich [8] quien demostró la validez de las tres propuestas y solamente dependía en cual sistema considerara la simultaneidad, como sucede con la dilatación del tiempo o la contracción del espacio. En el caso en que uno tenga en cuenta la simultaneidad en el sistema en reposo con el observador, donde se mide la temperatura, la transformación será la de Einstein-Planck con a = -1; en el caso en que uno mida la temperatura simultáneamente en el sistema en movimiento con respecto al observador, la transformación será la de Ott con a = 1; y en el caso en que uno mida las temperaturas de los cuerpos con la simultaneidad en sus propios sistemas de referencia, la transformación será la de Landsberg con a = 0.
Con todo, quedaban algunos puntos por discutir relacionados con las transformaciones de las otras cantidades termodinámicas. Un problema mayor consistía en cómo obtener las cantidades termodinámicas finales después de que dos sistemas termodinámicos con velocidades relativas relativistas se mezclasen o se pusiesen en contacto [9], [10], [11]. Así, entre las discusiones o paradojas más importantes, se puede citar la siguiente: consideremos a dos cuerpos en reposo con la misma temperatura y que se encuentran en dos sistemas con velocidades relativas relativistas. Considerando a la teoría de Einstein-Planck, el observador que se halla en reposo con uno de los cuerpos (cuerpo 1), lo ve con temperatura T0 y al otro cuerpo (cuerpo 2) que lleva una velocidad relativa con respecto al cuerpo 1, lo ve con temperatura igual a γ-1T0 conforme a la Ec. (1). Pero otro observador en reposo con respecto al cuerpo 2 verá al cuerpo 2 con temperatura T0 y al cuerpo 1 con temperatura γ–1T0. La pregunta es qué sucede si los ponemos en contacto termodinámico [12]: ¿El calor fluirá del cuerpo 1 al cuerpo 2 o al revés (ver Figs. 1a y 1b)?
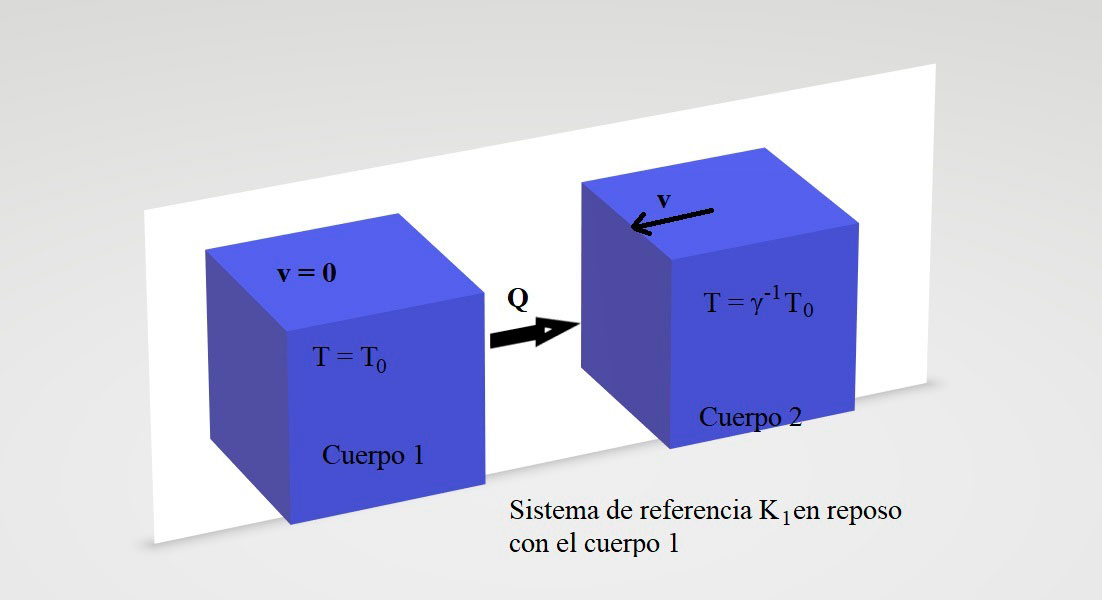
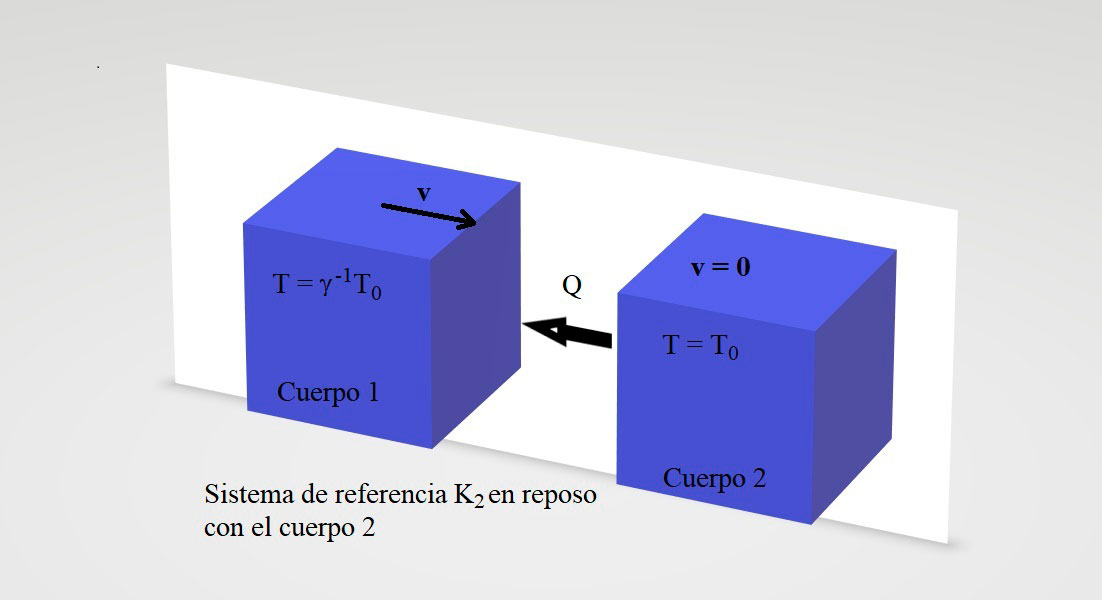
El problema se resuelve describiendo la forma de poner en contacto a los dos cuerpos. Existen varias formas de hacerlo según los sistemas considerados. Por ejemplo, propondríamos el caso de dos gases representando a los cuerpos 1 y al 2 y mezclarlos, o considerar la fusión de dos cuerpos negros [11] y muchos otros problemas que incluyen dificultades técnicas para resolverlos. Sin embargo, el resultado final dará siempre un sistema en equilibrio con una temperatura y una velocidad final.
Analicemos un caso muy sencillo para entender la transmisión del calor [12]. El sistema está compuesto de dos placas infinitas paralelas con una temperatura T0 con sus respectivos sistemas de referencia en reposo que se mueven a una velocidad relativa v (ver Fig. 2).
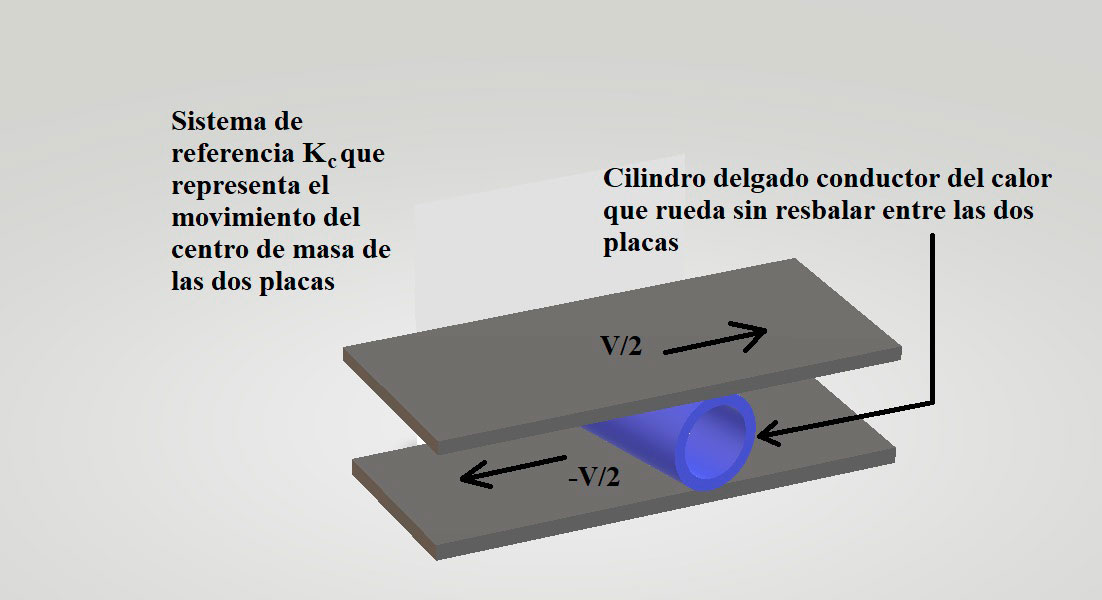
Las ponemos en contacto por medio de un cilindro hueco conductor del calor que rueda sin resbalar para evitar fricciones entre las dos placas. Las placas 1 y 2 están en reposo en los sistemas de referencia K1 y K2, respectivamente, con una velocidad relativa v. Como el cilindro rueda sin resbalar, gira con una velocidad angular constante y su centro de masa está en reposo en el sistema Kc que representará a un sistema de referencia tal que las dos placas se mueven a una velocidad v/2 y – v/2 con respecto al centro del cilindro (es decir, con respecto a Kc). En los dos puntos de contacto entre el cilindro y las placas, la velocidad relativa entre el punto de contacto y la placa es nula, pues el cilindro rueda sin resbalar tanto en el sistema K1 como en K2 y Kc, lo que implica que en los puntos de contacto siempre se tendrá la misma temperatura entre la placa y el cilindro; es decir: T0 en K1 para el punto de contacto de la placa 1 con el cilindro y T0 en K2 para el punto de contacto de la placa 2 con el cilindro. Por lo tanto, no existirá transmisión de calor y el sistema continuará con sus mismas propiedades termodinámicas.
En realidad, la gran dificultad que se presenta en sistemas con velocidades relativas no consiste en cuál modelo se utilice, sino en entender claramente cómo es la transmisión del calor para los distintos sistemas. En termodinámica se puede trabajar con cualquiera de las tres propuestas en tanto que se respete el concepto de simultaneidad seleccionado. Debe quedar claro que se deberá considerar la conservación de la energía y del momentum en cada sistema de referencia.
Por último, la física estadística de equilibrio permite resolver el problema, pues toma en cuenta los factores que se deben incorporar ahí donde se considere la simultaneidad. En hidrodinámica relativista se considera la temperatura en el sistema en reposo (comoving system) y los factores aparecen de manera natural.
Debemos comentar que en astrofísica existen implicaciones debido a la termodinámica relativista. En efecto, al momento de considerar un jet con velocidades relativistas que choca con otro plasma, se genera más calor de lo que se hubiese obtenido utilizando un esquema no relativista [10]. Existen también otras implicaciones importantes, como por ejemplo en la física de plasmas de quark-gluones, donde los efectos de la termodinámica relativista implican factores importantes en los tiempos de relajación [13]. Además, en la física del estado sólido, se sabe que el gradiente de la suma de los potenciales eléctricos y químicos es el responsable del flujo de electrones. Sin embargo, el flujo de entropía es conducido por la temperatura donde aparecerá el factor g-1 debido a la velocidad de los electrones y por lo tanto afectará el transporte de electrones. Por lo que, en vez de considerar solamente al potencial electroquímico, se deberá introducir el concepto de potencial termo-cinético ligado a la temperatura relativista. Acoplar estos potenciales implicará que, aunque el potencial eléctrico sea mayor en el cobre que en el aluminio, cuando un pedazo de cobre se junta con otro de aluminio no existirá el flujo de electrones [14].
Referencias
[1] Planck M 1908 Ann. Phys. (Lpz) 26 1
[2] Einstein A 1907 Jahrb. f. Rad. u. Elekt. 4 411
[3] Tolman R C 1934 Relativity Thermodynamics and Cosmology (Oxford: Oxford University Press)
[4] Jüttner F 1911 Ann. Phys. 34 856
[5] Liu C 1992 BJHS, 25, 185-206
[6] Balescu R 1968 Physica 40 309
[7] Sieniutycz S 1998 Phys. Rev. E 58 7027
[8] Rorhlich F 1966 Nuovo Cimento B 45 6200
[9] Noerdlinger P D 1967 Nature 213 1117-1118.
[10] Gonzalez-Narvaez R E, Ares de Parga A M and Ares de Parga G 2017 Annals of Physics 376 391–411
[11] Ares de Parga G, Ávalos Vargas A and López-Carrera B 2013 Entropy 15 1271-1288
[12] Herrmann F and Pohlig M 2021 Eur. J. Phys. 42 015607
[13] Ayala A, De la Cruz D, Hernández LA and Salinas J Phys. Rev. D 102, 056019
[14] Fuchs H U 2014 A Direct Entropic Approach to Uniform and Spatially Continuous Dynamical Models of Thermoelectric Devices (Energy Harvesting and Systems vol 1 Issue 3-4) pp 253-265