Diodos térmicos de cobre y pan de hojaldre

Foto de: ponk35

Uno de los mayores retos ambientales es limitar las pérdidas de calor causadas por la ineficiencia durante la producción, traslado y consumo de energía. Habitualmente, por cada Watt de potencia consumida efectiva, se requieren tres de potencia generada; los dos restantes se pierden en el ambiente en forma de calor. Si se recuperara una fracción de esas pérdidas, no sólo se reduciría el calor expelido al ambiente, también podría usarse para consumo humano. Una posible ruta es la utilización de dispositivos térmicos en estado sólido, en particular, rectificadores térmicos.

Hipotéticamente, un rectificador térmico es un mecanismo que presenta asimetría en la densidad de flujo de calor que transmite. Esto es, permite una mayor densidad de flujo de calor en un sentido que en otro, de manera análoga al funcionamiento de un diodo eléctrico. Estos instrumentos podrían tener un gran impacto en la recuperación de la energía perdida.

En la actualidad se han construido dispositivos donde se alternan capas nanométricas de sílice y alúmina, depositadas mediante un proceso conocido como erosión catódica por radiofrecuencia. El grosor de las capas va creciendo de 10 a 50 y finalmente 100 nm, para un espesor total de unos 200 nm. La rectificación, entendida como la relación entre la conductividad térmica medida en un sentido y otro, es de aproximadamente 3.3. Sin embargo, debido al espesor tan fino los gradientes de temperatura y los flujos de calor que puede soportar el dispositivo son muy pequeños. Además, la baja resistencia mecánica de la alúmina y la sílice limitan su escalamiento [1].

En este texto, compartimos los resultados obtenidos al procesar materiales metálicos en la búsqueda de diodos térmicos, que permitan recuperar al menos una fracción de la energía que se pierde en el  medio ambiente. Los metales son conocidos en general como excelentes conductores de calor y electricidad. En particular, el cobre es usado tanto en cables conductores de corriente eléctrica como en disipadores de calor. En números, el cobre puro tiene una conductividad térmica de aproximadamente 400 W/mK. Para tener un punto de comparación, el vidrio (considerado un aislante) conduce aproximadamente 1 W/mK. Y es precisamente esa conductividad la que se alcanza en materiales metálicos mediante el proceso que presentamos en este artículo.

Para explicar el proceso de fabricación y el origen de esta baja conductividad térmica, es preciso remitirnos a dos objetos que aparentemente no tienen nada que ver entre sí: las espadas de mil dobleces (tanto reales como ficticias) y la pasta de hojaldre.

 

Espadas y panes de mil dobleces

Comencemos por el pan de hojaldre. La diferencia de esta pasta con otras es que, al cortar el pan, se encuentran una serie de laminillas que remiten a un libro y aparecen al liberarse el agua de la mantequilla durante la cocción. ¿Y por qué le ocurre esto a esta masa?

El origen del hojaldre se pierde en la historia, aunque se considera que es de procedencia árabe y aparece por primera vez en el “Libro del arte de cocina”, publicado en 1607. Al contrario de una masa convencional, la mantequilla no se incorpora a la mezcla. En vez de eso, se coloca el trozo en medio de la hoja extendida de harina y agua. La hoja es entonces doblada sobre la mantequilla, se extiende con el rodillo y se vuelve a doblar. El número final de capas está dado por l=(f+1)ⁿ, donde f es el número de dobleces por paso y n el número de pasos. Se recomiendan 73 capas para hojaldre regular y al menos 729 para hojaldre fino.

Por otro lado, la técnica de fabricación de espadas conocida como Mokume gane (que se traduce aproximadamente como metal con granos de madera), fue desarrollada en Japón en el siglo XVII y recuerda a las también históricas espadas de Damasco. Originalmente se trabajaban metales suaves como el cobre o la plata mediante un proceso de fusión incipiente. En éste, se colocaban láminas alternadas de diferentes metales, generando una unión por difusión entre las láminas.

Posteriormente, se usó una ruta de forja donde las láminas se apilaban, se formaban a martillazos y doblaban sobre sí mismas para seguir golpeándolas y hacerlas más finas. Ambas rutas daban resultados similares, obteniendo un patrón muy particular como el observado en la figura. Esta técnica, además de utilizarse usada para espadas ornamentales, actualmente se usa en piezas de joyería. La idea de doblar mil veces sobre sí mismo el acero que forma la hoja de una espada fue retomada por George R. R. Martin, al describir las espadas construidas con acero Valyrio que aparecen en su serie de libros “Canción de fuego y hielo”, mejor conocidas como Juego de Tronos. Claro, además del patrón mostrado en la hoja, el acero Valyrio tiene propiedades mágicas propias del ambiente de la novela.

 

Unión por rolado acumulativo, ARB

Tal vez inspirado por las espadas Mokume gane, el investigador Yoshihiro Saito desarrolló la técnica conocida como ARB (Accumulative roll bonding, unión por rolado acumulativo) en 1991 [2]. En este proceso, dos láminas del mismo espesor se apilan cara a cara y se hacen pasar entre dos rodillos, con una reducción del 50%. Esto da como resultado una unión fría entre las dos láminas, generando una nueva pieza con la mitad del espesor y el doble de largo. La nueva lámina es cortada transversalmente a la mitad y las dos piezas resultantes vuelven a ser procesadas tantas veces como el material lo permita. El trabajo original de Saito demostró que era posible mejorar la resistencia del aluminio puro a niveles cercanos a los de sus aleaciones.

Una limitante del proceso propuesto por Saito es la inestabilidad de la microestructura. Los granos constituyentes de la aleación almacenan mucha energía debido a la considerable deformación, volviéndose inestables. Con suficiente tiempo o un poco de calor, la microestructura del material se revierte al estado inicial (mediante un proceso conocido como recristalización), perdiendo las mejoras conferidas por el proceso ARB.

A inicios de 2015 en la revista Advanced Materials and Processes, un grupo de trabajo liderado por Nathan Mara e Irene Beyerlein del Laboratorio Nacional de los Alamos, reportó una estrategia para superar este problema. Para ello utilizaron láminas de dos metales inmiscibles en el estado sólido: el niobio (Nb) y el cobre (Cu). Prepararon un emparedado donde una lámina de Nb de 1 mm de espesor estaba envuelta por 2 láminas de Cu de 0.5 mm cada una. Tras el proceso de ARB se obtuvo la unión de estos materiales disímiles. Posteriormente el proceso fue repetido con las láminas resultantes. Con este esquema cada paso genera nuevas interfaces, siguiendo una proyección exponencial de base 2. De este modo tras sólo 8 pasos, se tienen 256 interfaces y con 13 pasos se generan 8192 interfaces a través de un material laminado de 1 mm de espesor, con un largo y ancho de 15 y 10 cm respectivamente.

Naturalmente, la reducción en el espesor de las láminas sigue su propia secuencia reduciéndose por mitad en casa paso. Partiendo de láminas de 1 mm, tras 8 pasos se tienen espesores de laminillas de 4 micrómetros. Tras 13 pasos las láminas son, efectivamente, nanométricas. Con esta ruta es posible conseguir materiales nanométricos estables a partir de materia prima en el rango de milímetros. Cabe mencionar, que el tamaño de este tipo de productos era relativamente grande.

Mara y Beyerlein demostraron la estabilidad de las interfaces Cu-Nb usando microscopía electrónica de transmisión de alta resolución [3]. Evidenciaron también la estabilidad térmica de estos laminados, pues los granos de cada elemento no pueden atravesar las interfaces, por lo que se mantienen nanométricos. El principal resultado de este procesamiento, en términos de propiedades, fue la alta resistencia mecánica alcanzada, superior a 1 GPa, la cual es comparable con la de los aceros avanzados de alta resistencia y con de las aleaciones de titanio para aplicaciones aeroespaciales.

 

Nuestra contribución

En 2015 se adquirió un nuevo molino de laminación en la Unidad Saltillo de Cinvestav y de inmediato se buscó repetir los resultados de Mara y Beyerlein. Se consiguió alcanzar 13 pasos de rolado acumulativo y se comprobó la alta resistencia del material. De igual manera, se caracterizó el tamaño de las laminillas a medida que se reducía el tamaño de éstas, como se ve en la Fig. 2. Se trabajó también en el estudio de los mecanismos de separación de las interfaces durante la deformación de estos laminados, tema de una tesis de maestría. Una visita al Centro de Investigación en Materiales Avanzados (CIMAV) en Apodaca, Nuevo León, dio inicio a una línea de investigación.

El Dr. Jaime Álvarez Quintana ha trabajado por años en los fenómenos de transferencia de calor a través de interfaces en materiales donde las laminillas son nanométricas. Hace tiempo, estos materiales se desarrollaban usando técnicas de deposición física o química de vapor. Como se mencionó al inicio de este artículo, esto sólo permitía obtener unas 3 o 5 capas de materiales alternados SiO₂ y Al₂O₃. Ahora teníamos un material con miles de interfaces con laminillas nanométricas, así que de inmediato se midió la conductancia térmica a través del espesor.

 

Los resultados nos impresionaron. Los materiales prácticamente no conducían calor, con una conductancia térmica efectiva en el orden de 1 W/mK, muy cercana a la de un vidrio y muy alejada de la alta conductividad térmica del Cu (400 W/mK) y de la del Nb (80 W/mK). Estos resultados se presentan en la Fig. 3.

 

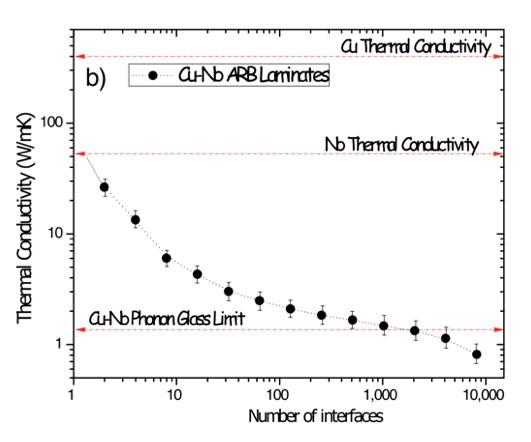
A partir de ahí hemos trabajado para entender los mecanismos que hacen que dos metales laminados juntos dejen de conducir a través del espesor. Recientemente reportamos nuestros hallazgos de que al irse reduciendo de grosor las laminillas y aumentar el número de interfaces, existen 3 regímenes de transferencia de calor.

En el primero, la caída en la conductancia térmica está mayormente causada por la irregularidad de las interfaces, ya que la unión entre las láminas no es perfecta. A medida que se aumenta el número de interfaces, se cree que la resistencia de contacto entre éstas es la responsable de la baja transferencia de calor, pero el efecto que lleva a reducir la conductancia térmica a los niveles reportados sólo ocurre cuando el espesor de las laminillas se acerca a la trayectoria media de los fonones responsables de la conducción de calor en el sólido. El ajuste de estos 3 regímenes propuestos con respecto a los datos experimentales aparece en la Fig. 4.

 

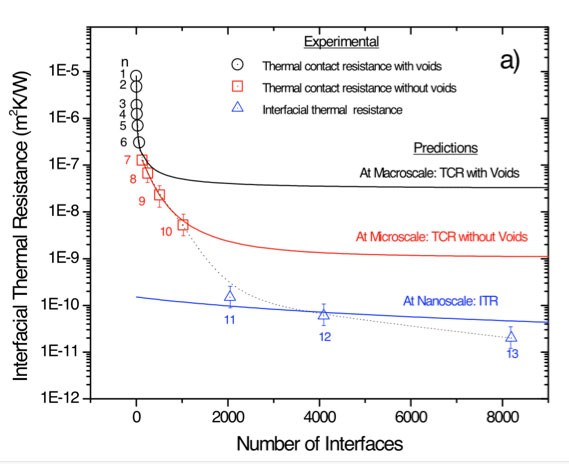
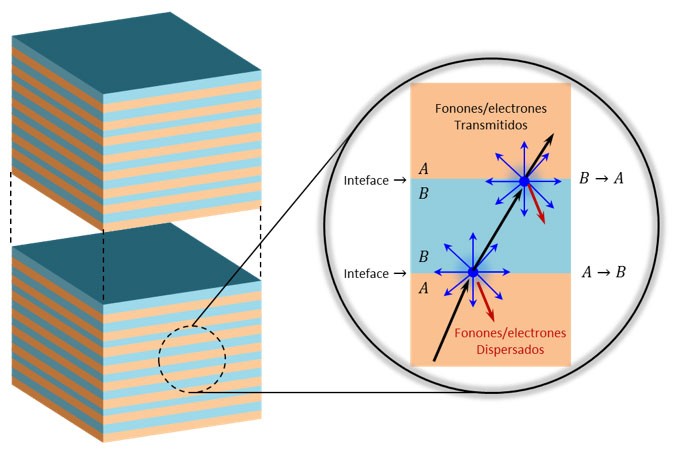
La resistencia térmica de interfaz formada entre dos sólidos disímiles como los mostrados en la Fig. 5 ha sido estudiada extensivamente (tanto experimentalmente como teóricamente) y se han propuesto varios modelos. De éstos, el modelo de desacople acústico AMM (Acustic Mismatch Model) y el modelo de desacople difusivo DMM (Diffusive Mismatch Model) son los más relevantes [5,6]. El modelo AMM supone que los fonones incidentes en una interfaz están sujetos a una reflexión o transmisión especular y se rigen por la mecánica continua, mientras que en el DMM la probabilidad de transmisión de fonones a cualquier lado de la interfaz depende de la proporción de la densidad de estados de fonones. De acuerdo con DMM, la resistencia térmica de interfaz se extiende en un rango de 10^-7 a 10^-9 m²K/W [5-7]. Por lo tanto, para poder apreciar un efecto significativo de la resistencia térmica de interfaz en la conductividad térmica el sistema de multicapas debe tener una longitud de período en nanómetros. De aquí que sistemas multicapas, con periodos del orden de los nanómetros pueden generar una alta densidad de interfaces, y con ello una considerable dispersión de electrones/fonones en cada interfaz, lo que resultaría en una drástica reducción de la conductividad térmica efectiva del sistema.

 

 

 

Perspectivas

En principio, tal vez pudiera parecer ocioso convertir a uno de los mejores conductores de calor (el cobre) en un material aislante. Pero no hay que olvidar que la resistencia de este material es tan alta como la de las aleaciones de titanio para aplicaciones aeroespaciales. De este modo, para las aplicaciones que así lo requieran, pudieran usarse láminas que funcionarían tanto como elementos estructurales como aislantes.

La perspectiva más interesante es la posibilidad de desarrollar diodos térmicos como los mencionados en la introducción a partir de la ruta descrita en este texto. En esa dirección se orienta el actual proyecto postdoctoral de la Dra. María Antonia Cardona, coautora de este artículo. Esperamos encontrar las condiciones de procesamiento que nos permitan obtener una variación periódica en el grosor de las laminillas a través del espesor del material laminado. Ello abriría un gran número de posibilidades para aplicaciones no sólo de aislamiento, sino de recuperación de calor.

 

 

Bibliografía

1. Tovar-Padilla, M., Licea-Jimenez, L., Pérez-Garcia, S. A. & Alvarez-Quintana, J. Enhanced performance thermal diode via thermal boundary resistance at nanoscale. Appl. Phys. Lett. 107, 2013–2016 (2015).
2. Saito, Y., Tsuji, N., Utsunomiya, H., Sakai, T. & Hong, R. Ultra-fine grained bulk aluminum produced by accumulative roll-bonding proces. Scr. Mater. 40, 795–800 (1999).
3. Carpenter, J. S. et al. Thermal stability of Cu–Nb nanolamellar composites fabricated via accumulative roll bonding. Philos. Mag. 1–18 (2012). doi:10.1080/14786435.2012.731527
4. García-Pastor, F. A., Montelongo-Vega, J. B., Tovar-Padilla, M. V., Cardona-Castro, M. A. & Alvarez-Quintana, J. Robust metallic nanolaminates having phonon-glass thermal conductivity. Materials (Basel). 13, 1–13 (2020).
5. Little, W. A.; The transport of heat between dissimilar solids at low temperatures. Canadian Journal of Physics 1959, 37, 334.
6. Swartz, E. T.; Pohl, R. O.; Thermal boundary resistance. Rev. Mod. Phys. 1989, 61(3), 605-668.
7. Reddy, P.; Castelino, K.; Majumdar, A.; Diffuse mismatch model of thermal boundary conductance using exact phonon dispersión. Appl. Phys. Lett. 2005, 87, 211908.

 

 

[1]

Dell 29/09/21 1:39 p.m.

exponemos