Resumen
Las imágenes médicas de zonas y tejidos del cuerpo humano se obtienen mediante diversas técnicas como: rayos X, tomografías computarizadas y por emisión de positrones, resonancia magnética y ultrasonido, entre otras. Éstas tienen un papel esencial en el diagnóstico y tratamiento de pacientes. Debido a las limitaciones de los dispositivos médicos, se obtienen con bajo contraste, baja intensidad, ruido, etcétera, complicando su uso con fines de diagnóstico; en consecuencia, para que los médicos realicen diagnósticos y tratamientos precisos es necesario que las imágenes sean mejoradas. Existen varios métodos para ello, entre los que destacan el ajuste de contraste, la ecualización de histogramas, los filtros de conservación de bordes y algunos más. En este trabajo se ilustra el uso del método de ecualización de histograma, el cual emplea algunas nociones estadísticas. Se presentan algunos ejemplos de la aplicación de esta técnica.
Introducción
En una cámara de video digital los sensores producen una salida eléctrica proporcional a la intensidad de la luz, en tanto que el digitalizador la convierte en datos digitales. De manera general, para obtener imágenes digitales se requiere de un sensor físico, el cual responde a la energía radiada por el objeto, y un digitalizador, que permite convertir la salida del sensor en un formato digital, es decir, la obtención de pixeles.
La salida de la mayoría de los sensores es una forma de onda de voltaje continuo cuya amplitud y comportamiento espacial se relacionan con el fenómeno físico que se percibe. Así, para crear una imagen digital se convierten los datos continuos del sensor a un formato digital; para ello se realiza un muestreo tanto de las coordenadas como de la amplitud, obteniendo un valor de intensidad en cada uno de los pixeles.
Modelo de color RGB
En el formato RGB cada color aparece con sus componentes espectrales primarios de rojo (Red), verde (Green) y azul (Blue). Ver Bhairannawar (2018).
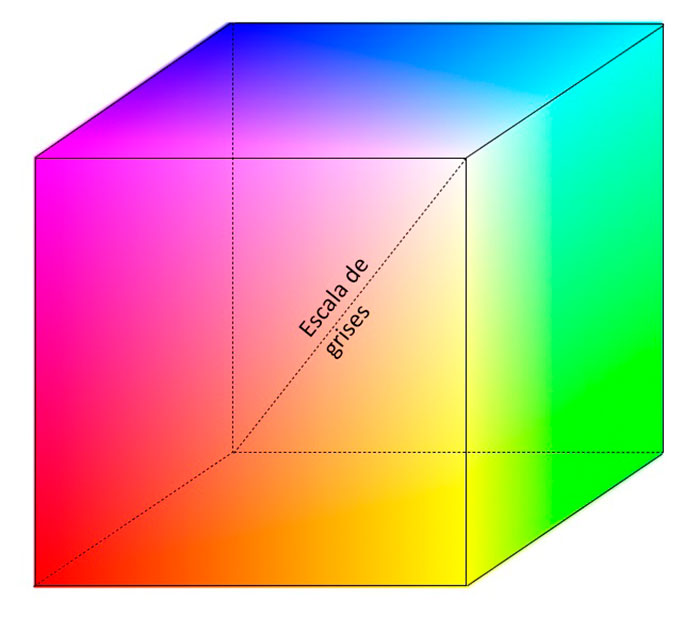
El sistema de coordenadas cartesianas es la base de este formato. El subespacio de color de interés es el cubo que se muestra en la figura 1, en el que los valores primarios RGB están en tres esquinas; los colores secundarios cian, magenta y amarillo se ubican en otras tres esquinas, el negro se halla en el origen y el blanco se sitúa en la esquina más alejada del origen. Por conveniencia se asume que las componentes se encuentran normalizadas, por lo que los valores posibles de R, G y B pertenecen al rango.
Modelo de color HSV
HSV es considerado un formato más cercano que el RGB a la forma en que las personas describen las sensaciones de color (Ibraheem et al., 2012). En este modo de color se consideran el tono o matiz (Hue), la saturación (Saturation) y el valor (Value). RGB no se distingue por ser muy intuitivo para crear colores en código, mientras que HSV reasigna los colores primarios RGB en dimensiones que se visualizan más fácilmente, ver figura 2.
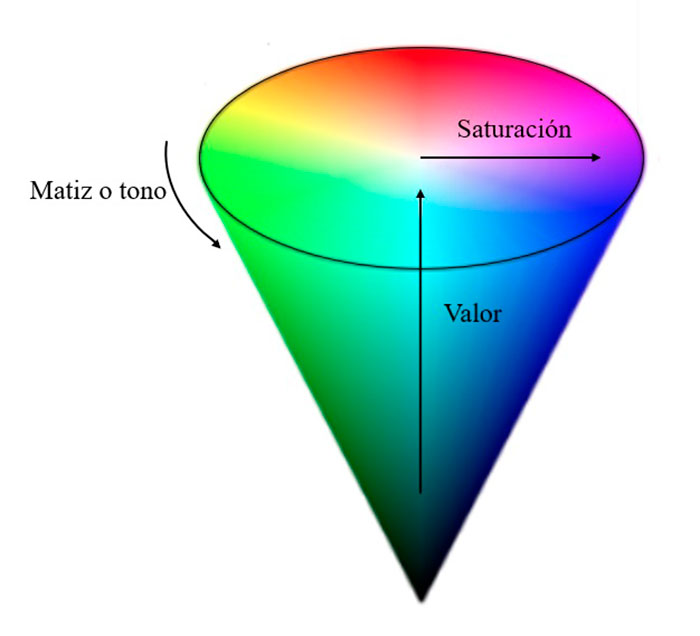
El tono se representa como un grado de ángulo con valores están entre 0° y 360° y cada cantidad corresponde a un color. 0°: rojo, 120°: verde, 240°: azul. Los grados intermedios corresponden a magnitudes intermedias.
La saturación controla la cantidad de color utilizada y se representa como la distancia al eje de brillo negro-blanco. Un color con una saturación del 100 % será el más puro posible, mientras que una saturación del 0 % producirá una escala de grises. A menor saturación, la tonalidad grisácea será mayor y el tono estará más decolorado.
El valor controla el brillo del color y representa la altura en el eje blanco-negro. Un color con 0% de brillo es negro puro, mientras que uno con 100% de brillo no tiene negro mezclado. Como la dimensión de valor frecuentemente es llamada brillo (Brightness), el modelo HSV a veces es referido como HSB.
Histograma de una imagen digital
Se consideran los histogramas como la base de numerosas técnicas de procesamiento en el dominio espacial y son ampliamente empleados en la mejora de imágenes digitales. El contraste se enriquece cuando se incrementa la diferencia entre sus tonos. Esto se puede realizar oscureciendo aún más los tonos oscuros al mismo tiempo que se aclaran más los claros; ello equivale a ampliar el rango de intensidades de pixeles.
Son deseables dos características en un histograma:
-
- Las intensidades de los pixeles se distribuyen uniformemente en todo el rango de valores, es decir, cada valor es igualmente probable.
- El histograma acumulativo aumenta linealmente en todo el rango.
El método de ecualización del histograma modifica la distribución de las intensidades de los pixeles para lograr estas características. Una descripción más precisa del método es:
Los niveles de intensidad de una imagen son valores enteros en el intervalo [0,L-1].
Usualmente se considera L de la forma L=2k y es muy común emplear k=8, es decir L=256.
Consideremos la variable aleatoria discreta X que representa la intensidad de los pixeles en una imagen de MN pixeles y representemos mediante nx la frecuencia con que ocurre la intensidad x en la imagen digital, para x=0, …, L–1.
La probabilidad de ocurrencia de los niveles de intensidad, es decir, la función masa de probabilidad de X puede estimarse mediante px(x)=nx/MN para x=o, …, L–1.
El histograma consiste en la representación mediante barras de la función px(x).
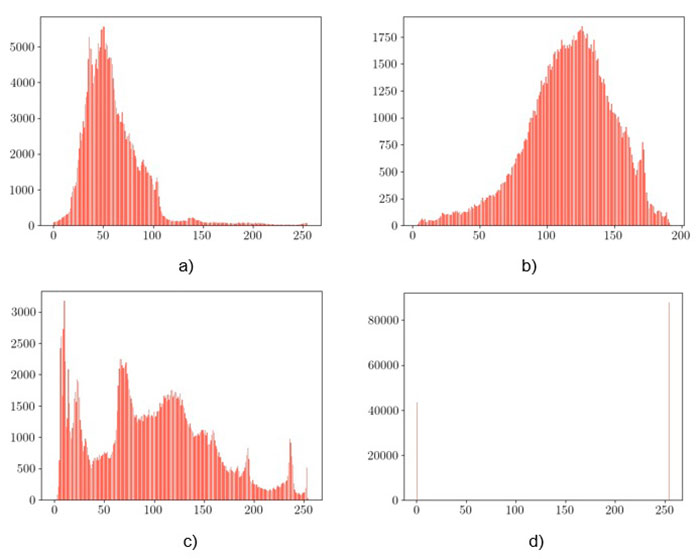
En la figura 3 se presentan cuatro imágenes con diferentes niveles de contraste y de iluminación, y en la figura 4 se muestran los histogramas correspondientes.

Para realizar la ecualización de histograma se efectúa la transformación siguiente:
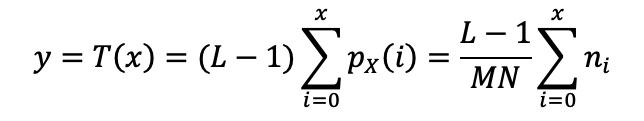
Así, el valor obtenido de y es un número real en el intervalo [0,L-1]; como el valor deseado es un número entero, los valores de y deberán redondearse al entero más próximo. Este valor se indicará por y*=T*(x). A continuación se ilustra el uso de la transformación.
Ejemplo 1.
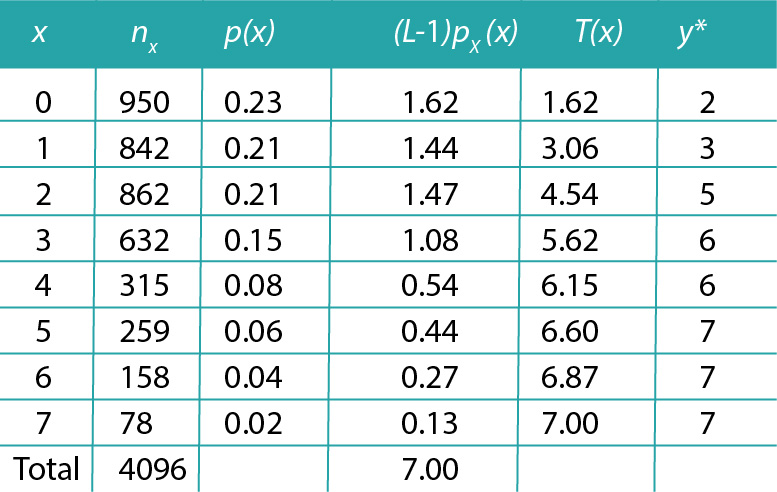
Consideremos una imagen con y pixeles con distribución de intensidad dada en la Tabla 1.
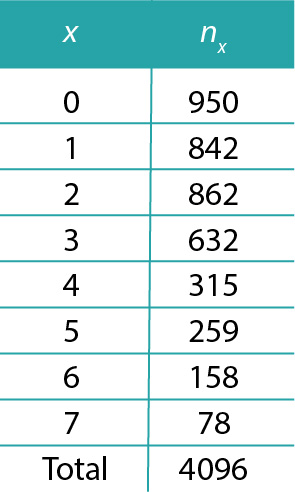
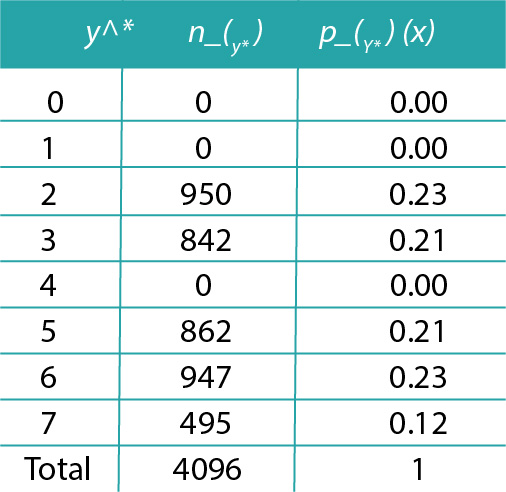
En la Tabla 2 notamos que, después de la transformación, a las intensidades 0, 1 y 4 no se les asignó valor alguno, mientras que a las intensidades 2 y 3, les fueron asignados 950 y 842 pixeles, respectivamente. A las intensidades 5, 6 y 7 les corresponden 862, 947 (632+315) y 495 (259+158+78).
Finalmente construimos la nueva distribución de intensidades en la tabla siguiente
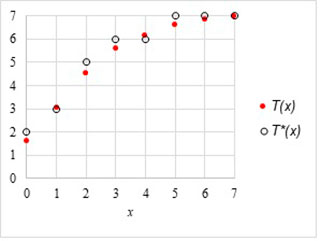
En la figura 5 se presentan la gráfica de la transformación T.
En la figura 6 se ilustran los dos histogramas.
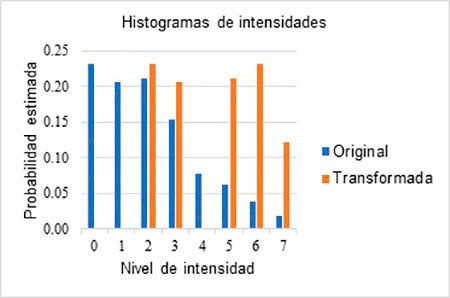
Como se aprecia, de las dos características deseables en un histograma, ninguna de ellas se logró plenamente, lo que se debe a que se trata con variables discretas y éstas presentan comportamientos discontinuos. Sin embargo, se observa que el histograma de las intensidades transformadas presenta una distribución más uniforme que el de las originales.
Mejora de imágenes médicas
En la figura 7 se exhibe una imagen de fondo de ojo, así como su versión mejorada después de aplicar el método de ecualización de histograma.
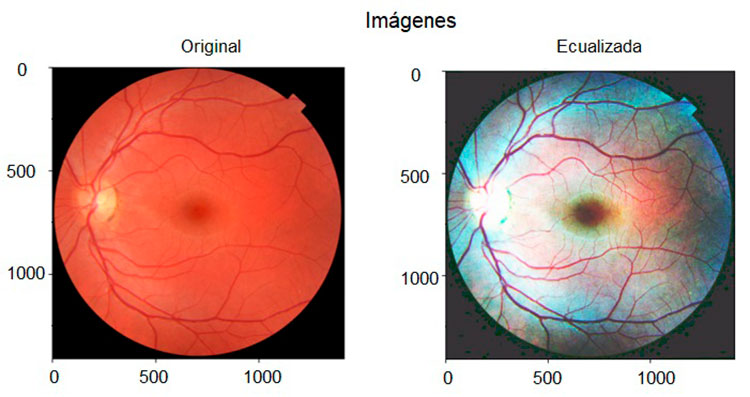
Para mejorar esta imagen se ecualizaron los tres canales de color en el modelo RGB.
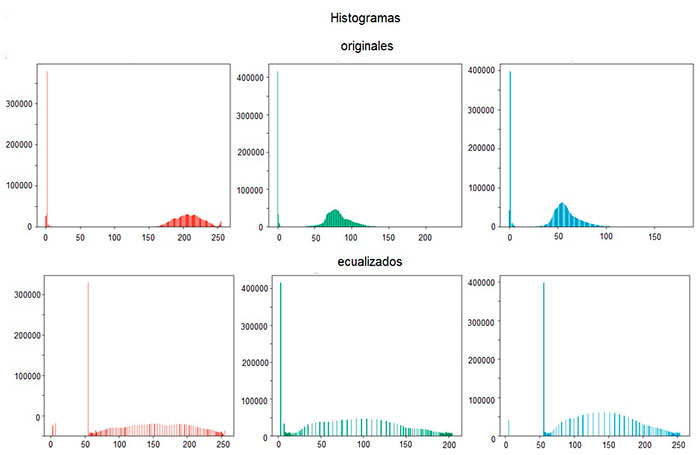
En la figura 8 se exponen los histogramas de los tres canales de color correspondientes a la imagen original, así como los respectivos histogramas de la imagen ecualizada. Se observa para cada canal una mejor distribución de los pixeles en los niveles de color, especialmente en el canal verde, el cual es de particular interés en este tipo de imágenes ya que en este se concentra la mayor información sobre el sistema vascular retiniano.
En la figura 9 se muestra una imagen de tórax obtenida mediante Rayos-X y su versión mejorada mediante el método de ecualización de histograma.
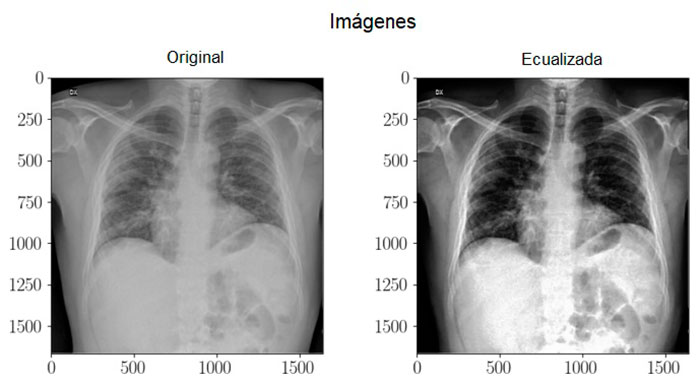
Para mejorar esta imagen se convirtieron los valores del modelo de color RGB al HSV, se ecualizó la componente de valor utilizando la transformación T y se transformaron los valores obtenidos en el modelo HSV al modelo RGB.
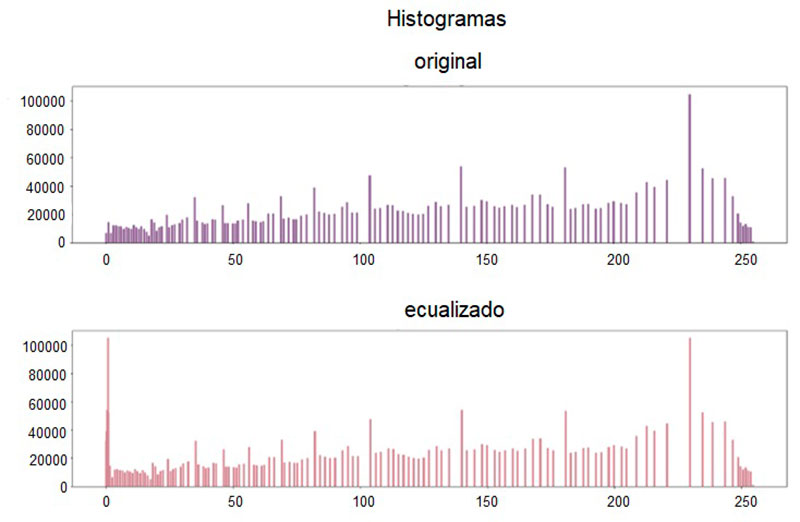
En la figura 10 se observa que en el histograma aumentó el número de pixeles oscuros y así se produjo mayor contraste que en la original.
Conclusiones
En este ensayo hemos presentado el método de ecualización de histograma. Dado que se aplica a la imagen completa, también es conocido como ecualización global de histograma. Este es un procedimiento simple y efectivo para incrementar de manera global el contraste de imágenes y ha probado ser de gran utilidad. Sin embargo, si la imagen contiene ruidos, también serán amplificados.
Existen variaciones de este método entre los que destacan el de ecualización adaptativa de histograma (AHE) y el de ecualización adaptativa de histograma con contraste limitado (CLAHE).
Bibliografía
Gonzalez, R., Woods, R., Eddins, S.L. (2004). Digital Image Processing. Upper Saddle River, New Jersey, United States, Pearson Prentice Hall.
Ibraheem N.A., Hasan M.M., Khan R.Z., Mishra P.K. (2012). Understanding Color Models: A Review. ARPN Journal of Science and Technology, 2 (3), 265-275.