Física, Matemáticas y Música: Aprendizajes de la Guitarra
Mi esposa y yo estamos convencidos de que la educación musical complementa de manera excepcional la formación académica de nuestros hijos. Por esta razón, los hemos inscrito en cursos vespertinos de iniciación musical, donde estudian materias como coro, solfeo —que también abarca teoría e historia de la música— y taller de instrumento. Además, practican deportes los días en que no tienen clases de música, siguiendo el proverbio: “mente sana en cuerpo sano”.
Al principio, pensamos en el piano para el taller. A diferencia de otros instrumentos, como el violín, el piano permite interpretar melodías comprensibles desde el inicio. Además, su amplio rango sonoro le permite tocar piezas sofisticadas sin necesidad de acompañamiento de otros instrumentos.
El problema surgió cuando nos informaron que era preferible contar con un piano grande en casa para que los niños pudieran practicar todos los días, incluso durante las vacaciones. Teniendo esto en cuenta, decidimos inscribirlos en clases de guitarra.
Es importante mencionar que la guitarra clásica es uno de mis instrumentos favoritos. Hace años compré una guitarra, pero nunca aprendí a tocarla. Ahora, aprovechando la oportunidad de ayudar a los niños con sus prácticas, he decidido comenzar a aprender también.
Una de las primeras cosas que me llamó la atención fue cómo sus pequeñas guitarras y la mía producen las mismas notas. Generalmente, se espera que los instrumentos más grandes emitan sonidos más graves, como ocurre con los instrumentos de viento.
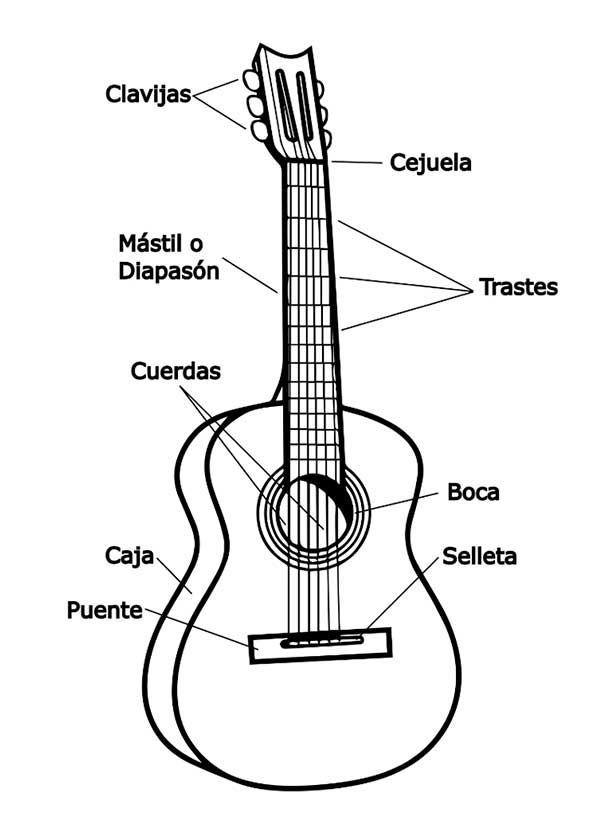En la carrera de física, estudiamos el comportamiento de una cuerda atada por sus extremos. Aprendimos que la frecuencia fundamental de oscilación depende del grosor, la longitud y la tensión de la cuerda: a mayor grosor, menor frecuencia; a mayor tensión, mayor frecuencia; y a mayor longitud, menor frecuencia. Esto explica cómo dos cuerdas del mismo grosor pueden producir la misma nota en guitarras de diferentes tamaños: las cuerdas de la guitarra más grande se tensan más para vibrar a la misma frecuencia. Esto aclara el primer misterio. Pero ¿qué ocurre con las notas producidas al pisar los trastes?
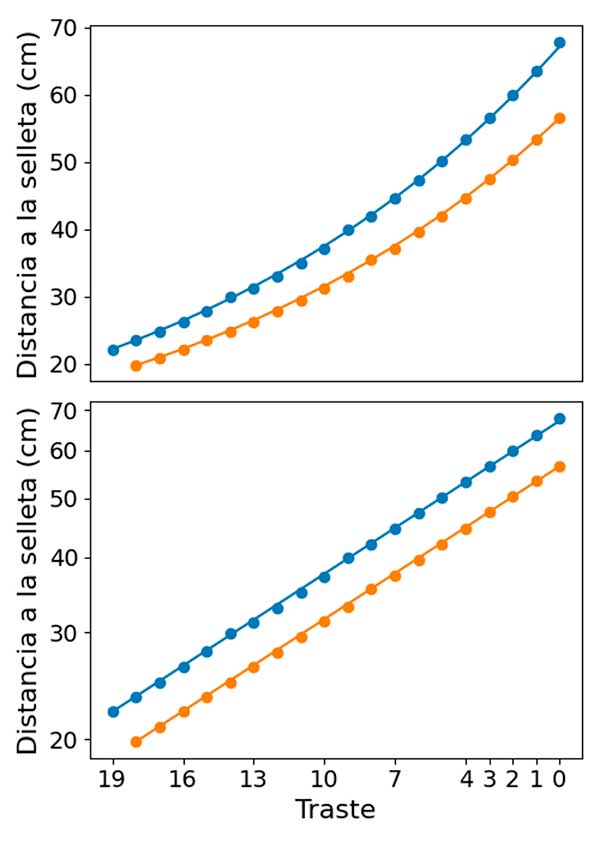
Para investigar esto, medimos la distancia entre la selleta y los diferentes trastes (Figura 1) en nuestras guitarras. Los resultados de nuestras mediciones se presentan en la Figura 2. En la gráfica del panel superior, se observa que, en ambas guitarras, la distancia entre trastes consecutivos aumenta a medida que nos alejamos de la selleta, aunque no parece haber una relación clara entre las mediciones de ambas guitarras.
Sin embargo, al cambiar el eje vertical a una escala logarítmica, los puntos de las dos guitarras se alinean a lo largo de líneas rectas con la misma pendiente. Matemáticamente, esto indica que el cociente de las distancias a la selleta de dos trastes consecutivos es constante (1.06 según nuestras mediciones) para cualquier traste y para ambas guitarras. En otras palabras, en ambas guitarras, la distancia desde la cejuela hasta la selleta es 1.06 veces la distancia del primer traste a la selleta; esta última es 1.06 veces la distancia del segundo traste a la selleta, y así sucesivamente.
Ya mencioné que la frecuencia del modo fundamental de oscilación de una cuerda con ambos extremos fijos depende de su longitud, siendo inversamente proporcional a esta. Al pisar la cuerda, se reduce su longitud, ya que los extremos permanecen fijos en la selleta y en el traste correspondiente, lo que provoca un aumento en su frecuencia. Considerando esto, los argumentos del párrafo anterior explican cómo dos guitarras de diferentes tamaños pueden producir las mismas notas. Solo es necesario ajustar la tensión para que una cuerda oscile con la misma frecuencia (f₀) cuando está libre. Luego, al pisar el primer traste en ambas guitarras, la cuerda vibrará con una frecuencia f₁ = 1.06 (f₀); al pisar el segundo traste, la frecuencia será f₂ = 1.06 f₁ = 1.062 (f₀); y así sucesivamente. Segundo misterio resuelto. Pero ahora surge la pregunta: ¿por qué el factor de 1.06 y no otro?
Utilizando el resultado anterior, observamos que la frecuencia al pisar el décimo segundo traste es f12 = 1.0612 (f₀) ≈ 2 (f₀). Esto significa que, después de 12 trastes, la longitud de la cuerda se reduce a la mitad y su frecuencia de oscilación se duplica. Dado que en una octava musical hay 12 notas (incluyendo tonos y semitonos: do, do#, re, re#, mi, fa, fa#, sol, sol#, la, la#, si), y que la misma nota en la octava superior tiene el doble de frecuencia, entendemos por qué se eligió el cociente 1.06: es aproximadamente igual a la raíz duodécima de 2. Así, al pisar trastes ascendentes, subimos en la escala musical, y al llegar al traste número 12, saltamos a la siguiente octava. Esto aclara la razón detrás del cociente 1.06, pero surge una nueva pregunta: ¿por qué hay 12 notas en una octava?
Desde la antigüedad, se descubrió que los sonidos cuyas frecuencias tienen cocientes que son fracciones de enteros armonizan bien entre sí y se utilizaron para crear música. Aunque la razón detrás de este fenómeno no se comprende completamente, se sospecha que se debe a que, cuando las frecuencias están relacionadas de esta manera, algunos de sus armónicos coinciden. Al vibrar una cuerda, no solo produce sonidos en su frecuencia fundamental, sino también en frecuencias que son múltiplos de esta, conocidas como armónicos.
Aunque en la antigüedad no existían instrumentos para medir frecuencias, se llevaban a cabo experimentos con el monocordio. Al pisar una cuerda tensa en puntos intermedios, la dividían en dos segmentos de diferentes longitudes y estudiaban el sonido de ambos segmentos.
Los griegos fueron de los primeros en formalizar este hallazgo. Por ejemplo, en el llamado modo jónico, al elegir una frecuencia base f₀, las siguientes frecuencias producen sonidos que armonizan bien con ella: (1 + 1/8) f₀, (1 + 1/4) f₀, (1 + 1/3) f₀, (1 + 1/2) f₀, (1 + 2/3) f₀, (1 + 4/5) f₀y 2 f₀. Los cocientes de frecuencias entre notas consecutivas del modo jónico (empezando con f₀) son las siguientes: 1+1/8, 1+1/9, 1+1/15, 1+1/8, 1+1/9, 1+2/25, 1+1/9. Como se puede observar, el penúltimo cociente rompe con el patrón establecido.
Esta discrepancia llevó a que, durante el Renacimiento, se sustituyera el modo jónico por la escala mayor, cuyas frecuencias son: f₀, (1 + 1/8) f₀, (1 + 1/4) f₀, (1 + 1/3) f₀, (1 + 1/2) f₀, (1 + 2/3) f₀, (1 + 7/8) f₀ y 2 f₀. En la escala mayor, los cocientes de frecuencias entre notas consecutivas son: 1+1/8, 1+1/9, 1+1/15, 1+1/8, 1+1/9, 1+1/8, 1+1/15.
En cualquier caso, si un instrumento se afina con las frecuencias del modo jónico o de la escala mayor, se pueden interpretar melodías agradables al oído. Sin embargo, las combinaciones son limitadas, y cambiar la frecuencia base requiere volver a afinar el instrumento.
Si escribimos los factores del modo jónico en notación decimal, obtenemos: 1, 1.125, 1.25, 1.33, 1.5, 1.67, 1.8 y 2. En tanto que los factores de la escala mayor son: 1, 1.125, 1.25, 1.33, 1.5, 1.67, 1.875 y 2. Al compararlas con las potencias de 1.06 del 1 al 12: 1.06, 1.12, 1.19, 1.26, 1.33, 1.41, 1.5, 1.59, 1.68, 1.79, 1.89, y 12, observamos que las potencias 2, 4, 5, 7, 9, 10 y 12 se aproximan bastante a los factores por los que se multiplica la frecuencia base en el modo jónico, mientras que las potencias 2, 4, 5, 7, 9, 11 y 12 se aproximan a los factores de la escala mayor.
Esto significa que dividir una octava en 12 intervalos equidistantes en la escala logarítmica (temperamento igual), permite aproximar bastante bien las notas del modo jónico y de la escala mayor, con independencia de la nota base elegida, sin necesidad de afinar constantemente el instrumento. Supongamos que la frecuencia base corresponde a do. Entonces, las notas que resultan de multiplicar dicha frecuencia base por las potencias de 1.06 del 0 al 12 son: do, do#, re, re#, mi, fa, fa#, sol, sol#, la, la#, si y do. De estas, las que se aproximan a las notas del modo jónico son: do, re, mi, fa, sol, la, la# y do, en tanto que las que se aproximan a la escala mayor son: do, re, mi, fa, sol, la, si y do. Por otra parte, si la nota base es fa, las notas del modo jónico serían: fa, sol, la, la#, do, re, re#, fa. En forma similar, las de la escala mayor son: fa, sol, la, la#, do, re, mi, fa.
La adaptación generalizada del temperamento igual en la música occidental a finales del siglo XIX, permitió estandarizar la fabricación de instrumentos musicales y la interpretación de la música. Si bien este sistema no reproduce con exactitud los intervalos naturales de los modos griegos, el temperamento igual facilita la modulación entre diferentes tonalidades y la interpretación de obras complejas en cualquier tonalidad utilizando el mismo instrumento afinado.
Anterior a esta estandarización, existían diversas afinaciones que, aunque más precisas en ciertas tonalidades, dificultaban la interpretación de piezas que modulaban entre varias tonalidades. El temperamento igual representó un notable avance al permitir la construcción de instrumentos con una afinación uniforme, facilitando el intercambio de partituras y la interpretación conjunta de agrupaciones musicales.
Esta convención extendida dio un gran impulso al desarrollo de la música occidental, popularizando el uso de instrumentos de teclado y removiendo barreras técnicas para la exploración armónica y la innovación musical. Si bien los sistemas de afinación alternativos aún se utilizan en ciertos estilos, el temperamento igual prevalece como el estándar universal en la práctica musical moderna.
La interconexión entre música, física y matemáticas es profunda y fascinante. A lo largo de la historia, estas disciplinas han estado intrínsecamente ligadas, especialmente en la Edad Media, cuando la música se estudiaba como parte de las matemáticas, bajo la convicción de que los principios matemáticos podían explicar las armonías musicales.
Los antiguos pensadores, como Pitágoras, comprendieron que las relaciones numéricas entre las frecuencias de las notas producían consonancias agradables al oído. Esta relación se manifiesta claramente en la física de los instrumentos musicales, donde la vibración de las cuerdas y la resonancia se describen con fórmulas matemáticas. Así, la música no solo es un arte, sino también una expresión de leyes físicas y matemáticas que rigen nuestro mundo, revelando patrones y estructuras que trascienden la mera creación sonora. Esta sinergia entre las disciplinas no solo enriquece nuestra comprensión de la música, sino que también nos invita a explorar la belleza inherente en los números y las frecuencias.
Los lectores interesados en profundizar en estos temas pueden consultar las siguientes referencias:
- French, R. M. (2009) Engineering the Guitar, Springer, ISBN: 9780387743684
- Isacoff, S. (2009) Temperament: How Music Became a Battleground for the Great Minds of Western Civilization, Knopf Doubleday Publishing Group, ISBN: 9780307560513