Los biólogos moleculares hablamos todo el tiempo de la información genética. Decimos que el genoma contiene toda la información necesaria para determinar las características de un ser vivo. ¿Qué queremos decir con ello? Y sobre todo, ¿qué relación existe entre el concepto de la información genética y la teoría de la información formulada por Claude Shannon?
La información genética
En 2010 el equipo de Craig Venter trasplantó el genoma de una especie de bacteria llamada Mycoplasma mycoides a otra similar de nombre Mycoplasma capricolum. Después de un tiempo, las bacterias de M. capricolum que recibieron el trasplante de genoma comenzaron a exhibir características de M. mycoides. Este experimento demuestra empíricamente uno de los paradigmas más importantes de la biología molecular, a saber: que las características físicas de un ser vivo las determina la información que contienen en su genoma.
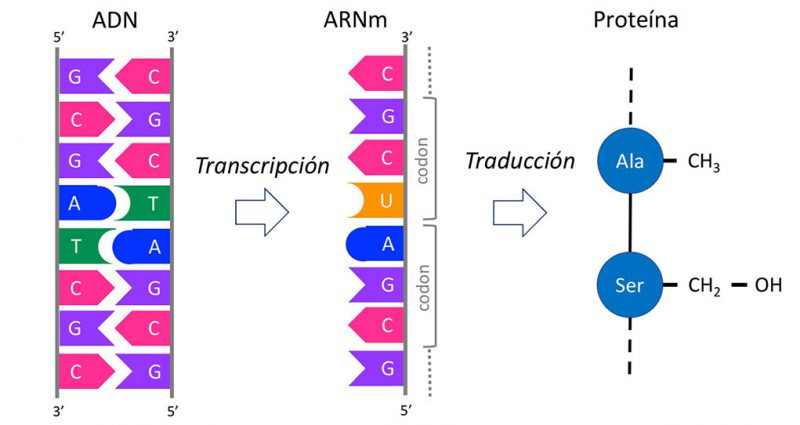
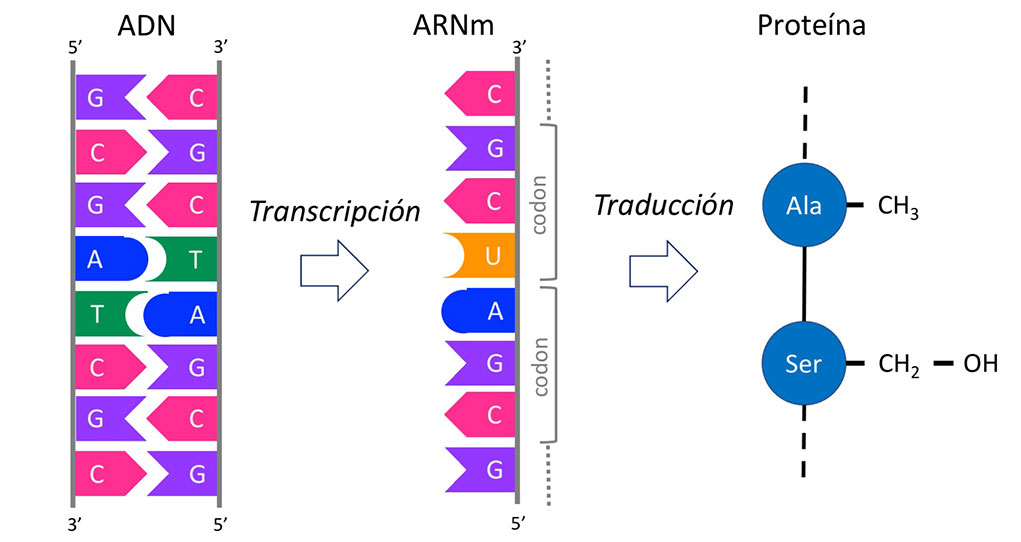
Para que un genoma determine las características de un ser vivo, es necesario que la información genética se exprese y luego se traduzca en proteínas (Figura 1). Los genomas contienen genes los cuales codifican para proteínas y son éstas las que llevan a cabo las diversas funciones celulares. Los genes se transcriben primero en ácido ribonucleico mensajero (ARNm) y después el ARNm se traduce en proteínas. Cada gen codifica para un tipo distinto de proteína y cada tipo tiene una función diferente.
La definición más empleada por los biólogos moleculares de un gen es: aquella secuencia de ADN que codifica para una proteína. A estos genes se les conoce como genes codificantes de proteínas. Sin embargo, puede haber otros tipos de genes, como aquellos que codifican para moléculas de ARN que no se traducen en proteínas. A estos se les llama genes no codificantes. Éstos producen moléculas de ARN que tienen diversas funciones, entre ellas, la de regular la expresión de otros genes.
Además, puede haber otro tipo de genes. Por ejemplo, se puede argumentar que una secuencia de bases del ADN que es necesaria para coordinar la expresión genética de otro conjunto de genes, es un gen en sí mismo. Por lo que, generalizando, pudiera decirse que un gen es cualquier secuencia de bases en el ADN que cumple una función requerida por la célula para sobrevivir o reproducirse.
Cuando los biólogos hablamos de la información genética de una célula o de un organismo, pensamos en el conjunto de genes codificados en su genoma. Éstos pueden tener desde unos pocos hasta varios miles. Por ejemplo, el SARS-CoV-2 tiene 29 genes, en tanto que el genoma humano un estimado de 20,000. La bacteria E. coli contiene aproximadamente 4,000, la mosca Drosophila melanogaster unos 14,000, la levadura Saccharomyces cerevisiae 6,000 y la planta Arabidopsis thaliana 25,000.
La teoría de la información de Shannon
Existe una teoría matemática de la información desarrollada por Claude Shannon (1948) a finales de la década de los 40, que permite cuantificar el contenido de información de un mensaje empleando la fórmula (Ecuación 1):
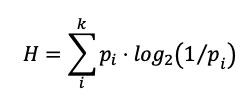
¿Qué encierra la fórmula de Shannon? Desde tiempos inmemoriales el ser humano ha tenido la necesidad de comunicarse, y lo ha hecho no sólo de manera oral sino utilizando símbolos. Éstos pueden representar objetos físicos simples (pictogramas) como un río, una montaña, el sol, hasta formas complejas y abstractas como los sentimientos o el dolor. En paralelo se desarrolló una escritura basada en pictogramas. El alfabeto surge a partir de asociar símbolos con sonidos, o simplemente simbolizar sonidos elementales. Su aparición permitió reducir el número de símbolos. Ello fue trascendental pues con el reducido espacio de símbolos comunes del alfabeto, es posible transmitir y almacenar diferentes mensajes, crear nuevos significados, y por tanto, difundir mayor información.
La escritura permitió, a través de los años, la transmisión de mensajes (papiros, códices, tablas). Sin embargo, era necesario propagar información en tiempo real. Por ejemplo, en la antigüedad, antes de iniciar una batalla era vital saber con cuántos soldados contaba el enemigo, saber si se podía sitiar una ciudad. La necesidad de enviar mensajes lo más rápido posible, dio origen a ingeniosos artefactos en el pasado. Después y gracias a la revolución técnica y científica en Occidente, el uso de los campos magnéticos y una adecuada codificación, permitió expedir mensajes a grandes distancias. Samuel Morse fue quien mejoró la velocidad de envío (código Morse) mediante el uso de puntos y rayas. Más adelante, Thomas Edison redefine el sistema y posibilita que el mensaje sea suficientemente grande para minimizar el efecto del ruido. Así comienza el concepto de medida de la información.
Inicialmente, Shannon encontró una mezcla de aleatoriedad y dependencias estadísticas en la comunicación humana. Observó que en un mensaje generalmente las palabras siguen un orden de precedencia, y utilizó los modelos de Markov para capturar esa estructura. Por ejemplo, en el idioma inglés (como en el español) algunas palabras son más frecuentes que otras; Shannon utiliza esta propiedad para cuantificar la cantidad de información de un mensaje a esa medida la llamó entropía.
Suponga que uno de sus colegas le ha transmitido una señal con una secuencia genética (utilizando sólo los símbolos de las bases: A, T, C, G); Digamos que su colega le envía la siguiente secuencia:
ACTGAACCTATTAAGAAAACATTTAAAAGTAATCAATGGA
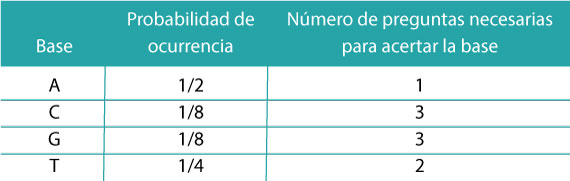
A continuación, usted puede conocer la frecuencia de cada una de las bases en la secuencia genética. Podríamos decir que esa frecuencia se aproxima a la probabilidad de que cada una de las bases ocurran. Éstas le ayudarán a calcular el contenido de información de la secuencia genética (Tabla 1).
Una vez que el colega le envió el mensaje, ¿cómo lograría saber cuánta información le fue enviada? Shannon ideó un árbol de preguntas [sí/no] para averiguarlo (Figura 2).
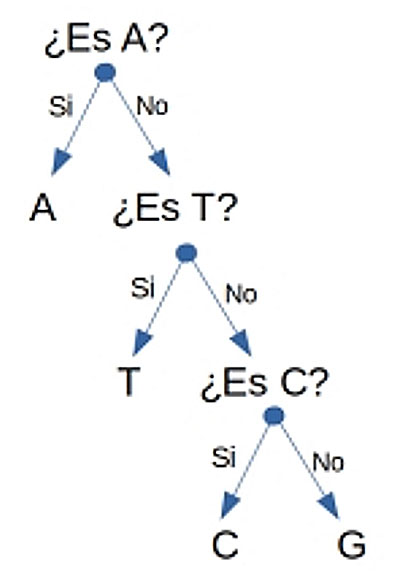
Digamos que usted recibe la primera base del mensaje. Dado que A es más probable de suceder (la probabilidad de ocurrencia es de 1/2), la primera pregunta será: “¿Es A?”; en caso de no serlo, la siguiente base más probable es T (su probabilidad es de 1/4) y entonces se preguntaría: “¿Es T?”; y si no fuese T, entonces se preguntaría si es “C” (alternativamente se puede preguntar si es “G”). Nótese que todas las preguntas tienen sólo dos posibles respuestas y que cada base se asocia a un número determinado de preguntas (por ejemplo, para encontrar la base “C” debemos de hacer 3 preguntas, Tabla 1).
Con este esquema, ¿cuál sería el número esperado de preguntas [sí/no] necesarias para acertar la primera base que el colega le envió? Será la suma del número de preguntas ponderada por su respectiva probabilidad de ocurrencia, es decir:
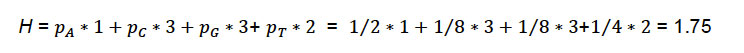
Shannon encontró que la relación del número de preguntas binarias necesarias para cada símbolo es igual a 𝑙𝑜𝑔2(1/p𝑖), donde p𝑖 es la probabilidad de ocurrencia del símbolo (base). Para la base C, se tiene que 3 = 𝑙𝑜𝑔2(1𝑝⁄𝐶)=𝑙𝑜𝑔2(8), sucediendo lo mismo para el resto de las bases. La unidad de medida de H son los bits (que proviene del inglés binary digits).
La entropía es máxima cuando todas las bases (los resultados del experimento) son igualmente probables y por tanto existe más incertidumbre. De manera inversa, cuando algunos resultados son más probables, la cantidad de incertidumbre disminuye. Es decir, hay menos posibilidades de sorpresas. La idea fundamental es: si la entropía de un mensaje disminuye, necesitamos hacer menos preguntas para encontrar el resultado.
¿Se puede utilizar la fórmula de Shannon para cuantificar el contenido de información genética que hay en un gen o un genoma? Es posible usar la fórmula para contabilizar ingenuamente el contenido de información que hay en un gen. Por ejemplo, tomemos el gen de 5SrRNA del cromatóforo de un protista que se llama Paulinella cromatophora:
TTCTATCCTGGTATCCATGGCGCTGTGGAACCACTCCGATCCATCCCGAACTCGGTTGTGAAACGCAGCA
GCGGCAACAATAGTTGGGGGGTAGCCCCCTGCGAAGATAGCTCGACGCCAGGTAAA
El gen 5SrRNA codifica para una molécula funcional de RNA que es fundamental para el funcionamiento celular, y el protista P. cromatophora, es una ameba muy particular pues contiene un cromatóforo, que es una cianobacteria endosimbionte que ha evolucionado en un plástido fotosintético. Si se toma y mide el contenido de información del gen utilizando la fórmula de Shannon, es decir, sustituimos en la ecuación 1 las probabilidades de las bases según van apareciendo tendremos:
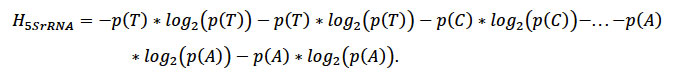
Es decir,
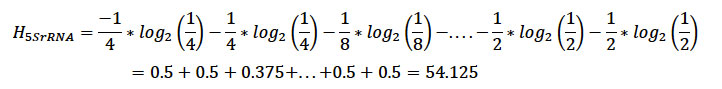
Si las 4 bases (A,T,G,C) estuviesen en la misma proporción, la entropía máxima Hmax es,
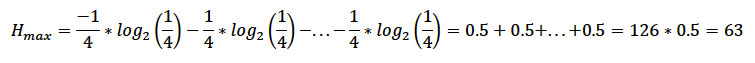
Con esta información es posible calcular la reducción en entropía (información) que contiene este gen con respecto a la máxima esperada (Ecuación 2):
![]()
En este caso ∆H = 8.875 (14.09% con respecto a la entropía máxima). ¿A qué se debe la reducción en la entropía con respecto a la máxima posible?
En biología el demonio de Maxwell es Darwin
Las secuencias de ADN que codifican genes no son aleatorias, es decir, contienen información que especifica la estructura de proteínas o de los ARN funcionales. En física, existe una metáfora creada por el físico escocés James Clerk Maxwell en 1867 para ilustrar la segunda ley de la termodinámica. La metáfora funciona de la siguiente forma: hay dos espacios contiguos cerrados. Ambos contienen un gas con la mitad de sus moléculas a una temperatura mayor que la otra mitad. Por lo tanto, la temperatura promedio de ambos espacios es la misma. Si se abre una pequeña compuerta entre los espacios para permitir que algunas moléculas pasen de un lado al otro de forma aleatoria, la temperatura promedio será igual en los dos espacios. En términos de la segunda ley de la termodinámica “En un sistema aislado la entropía nunca decrece”.
La segunda ley prohíbe que el calor se pueda transmitir de un cuerpo frío a un cuerpo caliente. La segunda ley se podría violar si existiera un pequeño demonio que fuese capaz de diferenciar las moléculas frías de las calientes. Este demonio, al controlar la compuerta entre los espacios, permitiría el paso de las moléculas frías en una dirección y el de moléculas calientes en la dirección contraria. Con el tiempo, la temperatura de un espacio sería mayor que la del otro. El demonio de Maxwell habría disminuido la entropía del sistema e incrementado la información.
En biología pensamos que las mutaciones en el ADN ocurren de forma más o menos aleatoria. Son el resultado de una infinidad de procesos moleculares. Sin embargo, no todas las que ocurren en un organismo se heredan a la siguiente generación. Existen dos procesos básicos que determinan el destino de las mutaciones. Uno es la deriva genética y el otro es la selección natural. Ésta actúa en cierto sentido como el demonio de Maxwell, permitiendo que solo ciertas mutaciones se hereden. Como resultado de la selección natural, la entropía de los genes va a disminuir.
Una reflexión final
La relación que pueda existir entre los genomas, la entropía y la información genética es mucho más compleja de lo expuesto aquí. En este ensayo hemos manifestado algunas ideas que esperamos inviten al lector a reflexionar un poco más al respecto. La naturaleza discreta de la información genética (el ADN se compone de cuatro bases: A, T, C, G) invita a utilizar herramientas matemáticas provenientes de otras áreas del conocimiento, en busca de mejor comprensión de los fenómenos biológicos, que son excepcionalmente complejos.
Referencias
- Descripción del demonio de Maxwell en la Wikipedia: https://es.wikipedia.org/wiki/Demonio_de_Maxwell
- El canal “The Art of the Problem” tiene una serie de videos sobre la teoría de la información de Shannon excepcionales: https://www.youtube.com/watch?v=p0ASFxKS9sg
- Página de la Wikipedia de Paulinella chromatophora: https://es.wikipedia.org/wiki/Paulinella_chromatophora
- Shannon, C.E. (1948). A Mathematical Theory of Communication, The Bell System Technical Journal, Vol 27, pp. 379-423.
Recuadro 1
¿Qué es un genoma?
Cuando los biólogos hablamos de un genoma, pensamos en el conjunto de moléculas de ADN distintas de un ser vivo. Podríamos pensar en un genoma como si fuese una biblioteca que se encuentra en el núcleo de cada célula. En el caso del genoma humano, la biblioteca está formada por 24 pares de libros. Cada uno representa un cromosoma; y para cada par de libros (cromosomas), uno fue heredado por la madre y el otro por el padre.
Cada cromosoma es una larga molécula de ADN (ácido desoxirribonucleico) que en determinados momentos del ciclo celular se enrolla en sí misma como si fuese un ovillo. El ADN, a su vez, es una doble cadena formada por la unión de dos hebras anti paralelas y complementarias. Cada una es una larga sucesión de moléculas elementales (digamos los eslabones de la cadena) de cuatro tipos básicos: Adeninas, Timinas, Citosinas y Guaninas. Estas moléculas las conocemos como las bases del ADN y las representamos con las letras A, T, C y G, respectivamente.
Las dos hebras anti paralelas del ADN se unen entre sí siguiendo las siguientes reglas de complementariedad: si en una de las hebras hay una A, en la otra debe de haber una T; y si en una de las hebras hay una G, en la otra deberá haber una C.
La información genética está codificada en el orden lineal de las bases (A, T, C, G) a lo largo del ADN. Y una sola molécula de ADN, es decir, un cromosoma, puede tener millones de pares de bases de longitud. Por ejemplo, el genoma de una bacteria como Escherichia coli tiene aproximadamente 4 millones de pares de bases.
No todo el ADN de un ser vivo codifica información genética, pues se limita a los genes y dependiendo del tipo de organismo, pueden estar contiguos o bien ampliamente espaciados por ADN no codificante.
Recuadro 2
Recordemos la definición del logaritmo de un número y sus propiedades.
La función logaritmo es la función inversa de la exponenciación, por ejemplo 1000 = 10*10*10 es: “3 es el logaritmo en base 10 del número 1000”, o expresado en forma matemática
log10(1000) = 3.
De manera general, el logaritmo de x en base b se denota como logb(x) donde la base puede ser explícita o no. Esta función es muy útil ya que simplifica operaciones matemáticas gracias a sus propiedades:
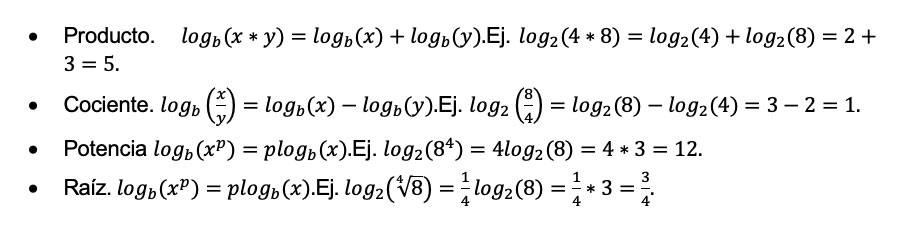
Y el cambio de base por ejemplo
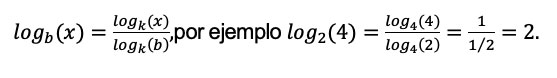
Algunas bases son más populares que otras, si b = 2 se le conoce como logaritmo binario (es el más usado en ciencias de la computación), si b = 10 se le llama logaritmo común y si b = e (constante de Euler, e ≈ 2.718) se le llama logaritmo natural.