La paradoja griega que trascendió a la física cuántica
Es bien sabido que a principios del siglo XX, las teorías existentes no podían explicar muchos de los fenómenos que se les presentaban a los físicos de la época. Uno de ellos surgió en la teoría clásica de la electrodinámica, la cual no fue capaz de estimar la cantidad de energía proveniente de la radiación térmica, ya que, basándose en dicha teoría, la energía que emitiría la vibración microscópica tendía a infinito. Otro hecho importante que contradecía los resultados esperados de la época se relacionaba directamente con la estabilidad de los átomos, ya que se pensaba que un electrón orbitando alrededor de un núcleo cargado debería emitir energía electromagnética disminuyendo su velocidad hasta caer sobre el núcleo, lo cual no sucede.
Así como éstos, muchos fenómenos no corresponden al resultado esperado; uno de los más importantes y contradictorios en nuestra experiencia, es el hecho de que un sistema no puede cambiar mientras se le esté observando, conocido como el efecto Zenón cuántico (QZE, por sus siglas en inglés quantum Zeno effect). Este efecto consiste en ralentizar la evolución temporal de un sistema físico, evitando la transición de un estado cuántico a otro mediante una serie de mediciones débiles e inmediatas.
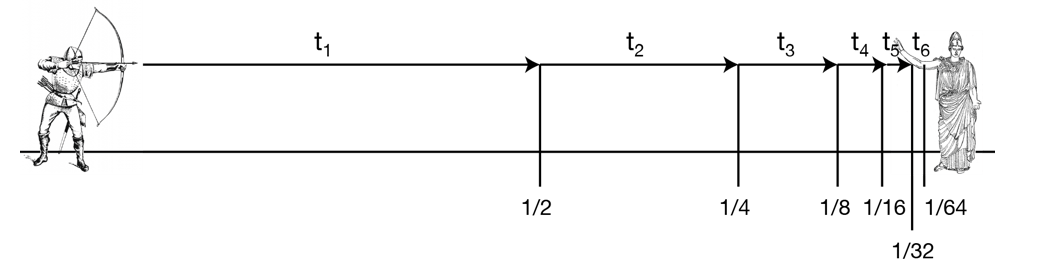
En la antigua Grecia, aproximadamente hace 2500 años, Zenón de Elea propuso una serie de paradojas dedicadas al problema del continuo y la relación entre el espacio, tiempo y movimiento. Quizás una de las más conocidas es llamada la flecha caminante. Esta paradoja se centra en el movimiento de una flecha en pleno vuelo. Zenón indicó que para cualquier instante en el tiempo “la flecha no se mueve de donde está, y tampoco se mueve a donde no está”. No puede moverse a donde no está porque no transcurre ningún tiempo; y no se mueve a donde está porque la flecha ya está ahí. Por lo tanto la flecha puede considerarse en reposo en ese instante. Entonces, para todos los instantes en el tiempo, la flecha también estará en reposo por el mismo motivo, lo que implicaría que el movimiento es imposible. Es contraintuitivo pensar que al lanzar una flecha, ésta nunca llegará a su objetivo, o que al observar un líquido en calentamiento este nunca llegue al punto de ebullición. Sin embargo, la física cuántica demostró que estas paradojas, consideradas filosóficas, son de hecho posibles. De allí el nombre que se le atribuyó al QZE.
Misra y Sudarshan [i] fueron los primeros en dar una demostración matemática formal de este efecto en 1977. En noviembre de 2017, su trabajo alcanzó alrededor de 1980 citas, mostrando así su trascendencia en la formulación cuántica contemporánea. Misra y Sudarshan describen el QZE mediante una partícula inestable que, observada continuamente, no decaerá siempre y cuando las observaciones sean a una escala de tiempo lo suficientemente pequeñas.
En 1990, Itano, Heinzen, Bollinger, and Wineland [ii] demostraron experimentalmente el QZE a partir de la inhibición de las transiciones entre estados cuánticos, basándose en un modelo para un átomo de tres niveles usando iones de berilio propuesto por R. J. Cook, en el cual el primero y segundo nivel energético son estables y el tercero decae al primer nivel mediante la emisión de un fotón. La inhibición de las transiciones entre niveles se debe a que la medición provoca un colapso en la función de onda tal que si el tiempo es lo suficientemente corto, la función de onda que describe al estado cuántico del sistema en estudio regresara al estado inicial.
En 2015 Patil y Chakram [iii] enfriaron un gas en una cámara al vacío expuesta a rayos láser. En ese estado, los átomos están ordenados como en un sólido cristalino. Pero incluso a temperaturas tan bajas, los átomos pueden moverse de un lugar a otro (efecto túnel). En este trabajo se demostró que mediante la observación es posible controlar el movimiento de los átomos. Una clara manifestación del QZE.
Estos trabajos fueron los precursores de estudios en sistemas cuánticos en los que se presenta el QZE mejorando la compresión del desarrollo del tiempo en esos sistemas. Además de las demostraciones latentes de la paradoja de Zenón a nivel cuántico se han encontrado distintas aplicaciones directamente relacionadas con el QZE, como son los sistemas de qubits superconductores, osciladores nanomecánicos, sistemas de espín desordenado, sistemas de átomos localizados, entre otros. El QZE también se usa para suprimir errores en implementación de óptica lineal y en computación cuántica.
El logro más reciente con este efecto es enviar información de un lado a otro del espacio sin necesidad de un vehículo que la transporte, un sistema de comunicación cuántica contrafactual. La contrafactualidad se define como la transferencia de un estado cuántico de un sitio a otro sin ninguna partícula cuántica o clásica transmitida entre ellos. Utilizando una fuente de un solo fotón se transfirió un mapa de bits monocromático de una ubicación a otra utilizando una versión anidada de QZE mediante una serie de interferómetros y fotodetectores que al detectar el fotón enviado evitaban que el sistema cambiara [iv].
Derivado del QZE, se puede definir también el efecto anti Zenón cuántico (QAZE), en el que las mediciones de hecho aceleran el proceso de evolución de un estado cuántico.
En 2001, Fischer, Gutiérrez-Medina y Raizen [v] afirmaron haber realizado la primera observación de QZE y QAZE, considerando átomos de sodio como un sistema cuántico inestable en una trampa magneto-óptica que sigue la ley de decaimiento exponencial. A partir de mediciones repetidas, el número de átomos se mantiene constante en la trampa o bien, decaen rápidamente dependiendo únicamente de la frecuencia con que se realice la medición.
Actualmente existe un desacuerdo respecto a cómo definir el QZE, ya que algunos autores distinguen entre la paradoja de Zenón Cuántica y el QZE. Cuando la frecuencia de las mediciones es finita y la evolución se ralentiza, se obtiene el QZE. En el caso límite en el que la frecuencia de las mediciones es infinita, un estado cuántico se encontrará “congelado” en su estado inicial. Es entonces cuando se tiene la paradoja cuántica de Zenón [vi]. Así también se considera que el QZE en realidad es una consecuencia de una perturbación del sistema observado causado por el mecanismo de observación.
Es difícil decidir si realmente es una paradoja que requiere de nueva física o simplemente es consecuencia de la, ya de por sí contraintuitiva, física cuántica ordinaria.
Referencias
[i] Misra B. and E. C. G. Sudarshan. (1977). The Zeno’s paradox in quantum theory. J. Math. Phys. 18. 756.
[ii] Itano W. M., Heinzen D. J., Bollinger J. J. and Wineland D. J. (1990). Quantum Zeno effect. Phys. Rev. A. 41 2295.
[iii] Patil Y.S., Chakram S., Vengalattore M. (2015). Measurement-Induced Localization of an Ultracold Lattice Gas. Phys. Rev. Lett. 115 (14).
[iv] Cao, Y., Li, Y. H., Cao, Z., Yin, J., Chen, Y. A., Yin, H. L. & Pan, J. W. (2017). Direct counterfactual communication via quantum Zeno effect. Proceedings of the National Academy of Sciences, 114(19), 4920-4924.
[v] Fischer, M. C., Gutiérrez-Medina, B., & Raizen, M. G. (2001). Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Physical review letters, 87(4), 040402.
[vi] Itano, W. M. (2009). Perspectives on the quantum Zeno paradox. In Journal of Physics: Conference Series (Vol. 196, No. 1, p. 012018). IOP Publishing.
Karen Atzín Meza Martínez