La simetría gauge: reveladora de interacciones fundamentales
En la primera parte de este artículo repasamos cómo las ecuaciones de Maxwell (eM), que describen la electrodinámica clásica, tienen cierta simetría “de gauge” que se manifiesta al escribirlas en términos de los potenciales eléctrico y magnético. En la segunda, destacamos que se puede deducir las eM requiriendo invariancia gauge. Así, descubrir la interacción a partir de la simetría constituye un cambio de paradigma que ha permitido deducir correctamente las leyes físicas para las interacciones débiles y fuertes que – junto a la electrodinámica cuántica- conforman el llamado Modelo Estándar de partículas elementales (ME). Hay argumentos convincentes para pensar que la teoría que generalice el ME a energías mayores también será de gauge, no así para la que unifique el ME con la Gravedad.
El trabajo de brillantes científicos entre los que destacamos a Coulomb, Gauss, Ampère o Faraday entre los siglos 18 y 19 culminó con las eM, que unifican electricidad, magnetismo y óptica en el electromagnetismo, entorno a 1870. Además, contienen el embrión de la relatividad especial, que se desarrollaría a principios del siglo 20.
En el sistema natural de unidades, las eM se escriben:[1]
∇E = ρ , ∇B = 0 ,
∇ × B − ∂t E = j , ∇ ×E + ∂t B = 0 (1).
Las dos primeras ecuaciones nos dicen cómo son las líneas de campo eléctrico (E) y magnético (B): abiertas en el primer caso y cerradas en el segundo, lo que concuerda con la existencia de cargas eléctricas, con densidad ρ, e inexistencia hasta donde sabemos de monopolos magnéticos. Esto último corresponde a una experiencia familiar: al dejar caer limaduras de hierro en una hoja bajo la que hay un imán éstas se distribuyen creando líneas cerradas, que entran y salen del mismo por sus polos. Un experimento semejante con cargas eléctricas muestra que éstas son fuentes/sumideros de las líneas, abiertas, de campo.
En la tercera encontramos la gran aportación de Maxwell, añadir una corriente de desplazamiento (dependiente de la variación temporal, ∂t, del campo eléctrico) para garantizar la conservación de la carga eléctrica, donde j es la corriente debida al movimiento de los electrones. La última ecuación es la ley de Faraday-Lenz y explica la inducción electromagnética, según la cual se puede generar un voltaje por medio de campos magnéticos variables en el tiempo.
Las eM son intrínsecamente relativistas, por lo que no es de extrañar que su escritura se simplifique en la notación que exhibe su simetría. Son invariantes ante las llamadas transformaciones de Lorentz, no de Galileo[2], lo que garantiza la constancia de la velocidad de la luz en vacío para todos los observadores con velocidad relativa constante entre sí. Por ello se dice que son covariantes Lorentz. En la misma, los objetos utilizados son vectores con cuatro componentes, una temporal y tres espaciales, llamados 4-vectores y objetos de dos índices (cada uno con cuatro componentes espacio-temporales también) con transformaciones fijas bajo el grupo de simetría (que los caracterizan como tensores). En esta notación conveniente, aunque más compleja matemáticamente, las eM se escriben de manera compacta como solo dos ecuaciones –juntando las que tienen segundos miembros nulos o no, respectivamente-.
En esta notación, la conservación de la carga eléctrica proviene de la correspondiente conservación de una 4-corriente y es una condición de compatibilidad de las eM. En su forma tradicional, las ecuaciones (1) permiten reemplazar los campos E y B, por dos potenciales: uno escalar (ϕ) y otro vector (A). De esta forma, se pasa de 6 componentes (tres de cada campo) a 4 (ϕ, y 3 de A). Este cambio conlleva que estos potenciales no estén unívocamente definidos y que los observables físicos sean invariantes bajo transformaciones de los mismos, llamadas “de gauge”, cuya forma es covariante. Desde (1) podría parecer que los potenciales electromagnéticos son un simple truco matemático para simplificar las eM, sin realidad física. El efecto Aharonov-Bohm, en mecánica cuántica, en el que una partícula cargada se ve afectada por potenciales electromagnéticos no nulos (a pesar de anularse E y B en la región de interés), evidencia desde mitad del siglo pasado la realidad física de los potenciales ϕ y A. Usándolos para escribir las eM, su invariancia gauge es inmediata. Las transformaciones de gauge, en la notación de la ec. (1), son
A → A+ ∇ f, ϕ → ϕ- ∂t f (2),
donde f es una función con dependencia espacio-temporal de variaciones suaves.
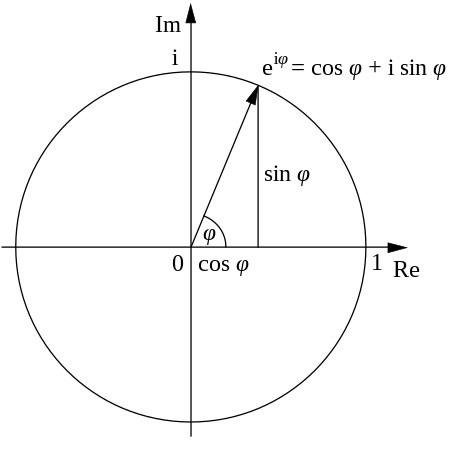
En nuestra segunda perspectiva, partimos de la ecuación de campo clásica que describe una partícula como el electrón (la ecuación de Dirac, eD, 1928) y comprobamos que al componerse de términos donde aparece el producto del campo complejo por su conjugado[3], siempre podemos hacer una transformación (T) de fase constante al campo, que será compensada por la T con la fase opuesta de su conjugado, de modo que las ecuaciones queden invariantes. Este grupo de T de simetría, son las llamadas U(1), donde la U proviene de que conservan las probabilidades (son “unitarias”) y el 1 hace referencia a su número de generadores (o parámetros que definen la T), que en este caso puede verse como un ángulo. Esto es trivial si el campo complejo se escribe en su forma módulo-argumento (véase la figura 1). Al ser una simetría continua, en aplicación del teorema de Emmy Noether, 1916, le corresponde una 4-corriente, con su carga respectiva (en este caso es la eléctrica), ambas conservadas.
La teoría cuántica de campos combina, desde 1926, la relatividad especial y la cuántica, por lo que no es natural una T de fase idéntica en todos los puntos del espacio-tiempo. Esto requeriría propagación instantánea de señales, lo que viola causalidad, al tener en cuenta la velocidad finita de propagación de la luz. Por ello sería deseable que la invariancia U(1) pudiera ser local, es decir, con una fase que dependiera del punto espacio-temporal. Esto no es inmediato, ya que las derivadas espaciales y temporales (∇ y ∂t en (1)) hacen que la eD no sea simétrica bajo esta T local. Aquí es donde surge el principio de gauge, que nos dice que una vez identificada la simetría bajo T constantes, “globales”, para la materia (a través de la eD para electrones, p. ej., con simetría U(1)), debe garantizarse que se preserve cuando éstas sean variables (“locales”). Ello requerirá la introducción de campos “de gauge” dinámicos, con propiedades de T determinadas. Como resultado de este proceso, se genera la interacción corroborada experimentalmente entre la materia y los mediadores. Esto sucede según el llamado “acoplamiento mínimo”, por el que el 4-campo del fotón se acopla a la 4-corriente conservada de Noether que garantiza la constancia de la carga eléctrica.
El principio de gauge permite entender, desde la simetría, la prescripción de acoplamiento mínimo, según la cual, en presencia de electromagnetismo, el operador que codifica la dinámica del sistema p2/(2m) -donde el momento p no es necesariamente el producto de la masa m por el vector velocidad- debe cambiarse a (p-eA)2/(2m)+eϕ, y las cargas eléctricas se miden en múltiplos de e.
Es maravilloso que las ecuaciones así obtenidas (eD, junto con el término de propagación de los fotones y el de acoplamiento mínimo) reproduzcan las eM y garanticen la conservación de la carga eléctrica: todo ello a raíz de pedir que la simetría U(1) global de la eD fuera local, según requiere el principio de gauge. Esa misma simetría explica por qué el fotón no tiene masa, ya que violaría invariancia gauge, y se refleja en el alcance infinito de esta interacción. Debido a esta invariancia bajo transformaciones U(1) locales, la electrodinámica cuántica puede estudiarse con un nivel de precisión extraordinario (en el caso del factor giromagnético del electrón, que describe su interacción dipolar magnética, llega hasta la duodécima cifra decimal en el acuerdo entre medida y predicción del ME).
Esta nueva perspectiva es hermosa: se ha re-deducido el electromagnetismo a partir del principio de gauge local usando la simetría U(1), pero su belleza es todavía mayor atendiendo a su utilidad, ya que aplicar el principio de gauge (con grupos de simetría locales específicos, más complicados y no conmutativos, como lo son las rotaciones en el espacio tridimensional) predice exactamente las interacciones débiles y fuertes, que junto a la electrodinámica constituyen desde hace sesenta años el ME, la mejor descripción conocida al nivel más fundamental. El ME es válido hasta energías equivalentes a mil millones de veces la masa del protón, a las que se realizan las colisiones entre estas partículas en el Gran Colisionador de Hadrones, LHC, por sus siglas en inglés. Las interacciones predichas por el ME han sido corroboradas con una enorme cantidad de medidas con precisión creciente, apoyadas en cálculos con incertidumbres parejamente pequeñas, desde su postulación. Usar este principio lleva a teorías consistentes al considerar sus correcciones cuánticas, lo que es un requisito para aquellas que puedan generalizar el ME a energías todavía mayores que las que han sido probadas actualmente. Por ello, dentro del marco de las teorías cuánticas de campo, pensamos que el siguiente avance en la comprensión del Universo en escalas de distancia (energía) cada vez menores (mayores) venga de la mano de una teoría de gauge. No obstante, sabemos que la cuántica de campos es incompatible con la relatividad general, por lo que quizá la teoría que englobe a ambas se deduzca de principios de simetría más fundamentales que el aquí expuesto.
Agradecimientos: agradezco a los estudiantes de servicio social, maestría y doctorado que han leído desinteresadamente este texto y al comité editorial de AyP, que me han dado una retroalimentación muy útil para mejorarlo.
[1] Las magnitudes en negrita como el operador diferencial ∇, son de tipo vectorial: tienen tres componentes, una en cada dirección espacial.
[2]Las leyes del movimiento en la mayoría de situaciones ordinarias (carros, pelotas, etcétera) son simétricas bajo transformaciones de Galileo, pero cuando las velocidades involucradas son tan grandes que resultan comparables a la de la luz, son las de Lorentz (que tienen como límite de bajas velocidades a las de Galileo) las que deben usarse.
[3]Uno aniquila partículas y crea antipartículas, y viceversa. Ambos son necesarios para entender procesos como la aniquilación de un par electrón-positrón (antipartícula del electrón) a fotones, en la que se fundamenta la prueba de imagen médica conocida como tomografía por emisión de positrones, y que se usa para diagnosis e investigación.
Portada: Líneas de fuerza de dos cargas iguales, realizadas con limadura de hierro y pintura en aerosol. Creative Commons. Author: Netoloco