Método de factorización y grafeno: la máquina de Mielnik
El carbono es el cuarto elemento más abundante de la Vía Láctea; en la tierra lo encontramos tanto en estado puro como en compuestos orgánicos e inorgánicos. Los átomos de carbono se pueden unir entre sí de distintas formas, cada una de las cuales es conocida como alótropo. De éstos ya se conocían desde la antigüedad el diamante y el grafito; posteriormente, en la era moderna se descubrieron los fulerenos y los nanotubos, que corresponden a estructuras esféricas y cilíndricas respectivamente (Figuras 1a y 1b). En 1947 se predijo la existencia de un alótropo de carbono faltante, el cual fue llamado grafeno [1] (Figura 1c). Fue hasta 2004 que los físicos Novoselov y Geim lograron aislar en el laboratorio una monocapa de grafeno a temperatura ambiente.
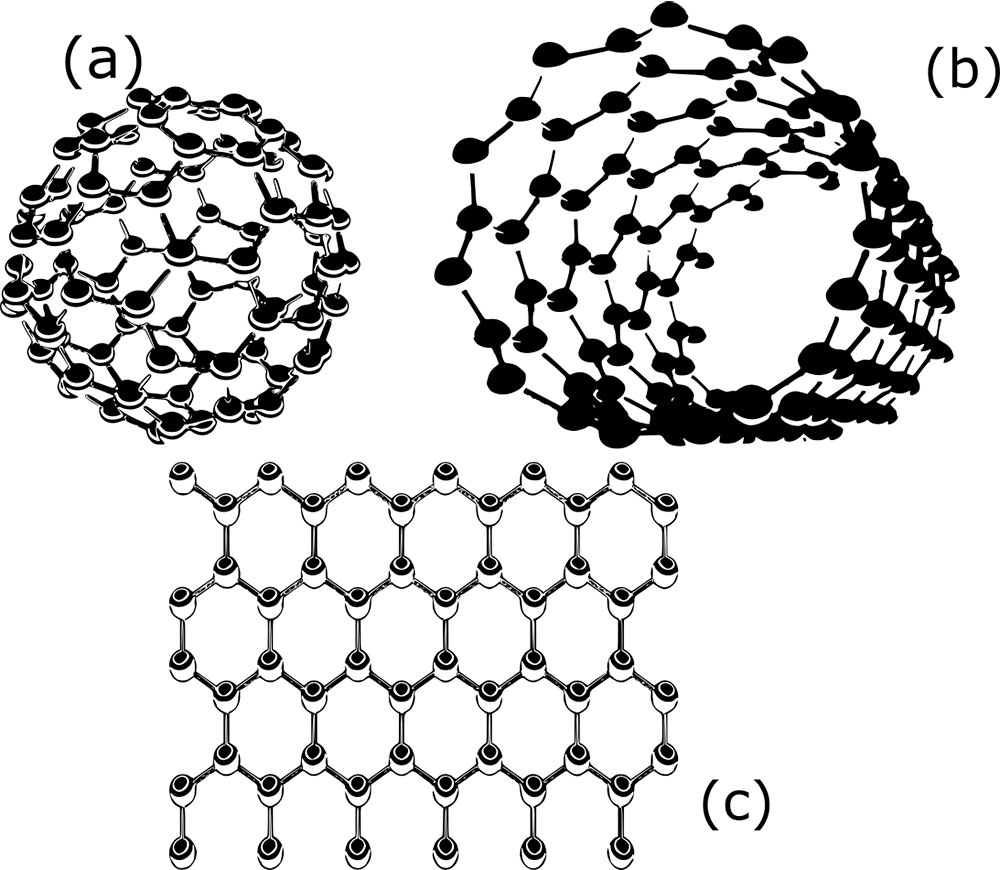
(b) nanotubos de carbono, (c) grafeno.
El grafeno es un material que puede considerarse bidimensional, formado por solo una capa de átomos de carbono distribuidos de manera hexagonal, como se muestra en la Figura 1c. Los portadores de carga en este material tienen una alta movilidad, por lo que es un buen conductor eléctrico. Además, tiene una alta resistencia mecánica y a su vez es flexible. Algunos autores mencionan una flexibilidad del grafeno hasta del 25% con respecto a su forma original. Una de las propiedades ópticas más importantes es su trasparencia, reteniendo únicamente un 2% de la luz que pasa a través de él. Todas estas propiedades hacen que el grafeno sea un material muy prometedor en la construcción y mejoramiento de pantallas de teléfonos celulares, baterías y partes de avión, entre otros dispositivos.
El descubrimiento del grafeno ha impulsado el estudio de nuevos materiales bidimensionales, como el borofeno, germaneno, fosforeno y otros; compuestos por distintos átomos. Además, es importante analizar el apilamiento de algunas monocapas de grafeno, siendo de gran interés la bicapa y la tricapa.
El arreglo hexagonal que caracteriza al grafeno se puede subdividir en dos subarreglos triangulares A y B, como se muestra en la Figura 2. Para analizar la monocapa de grafeno se usa como modelo físico la aproximación de amarre fuerte a primeros vecinos, la cual solo considera las interacciones de un átomo tipo A (B), con sus tres vecinos más cercanos, del tipo B (A). A bajas energías este modelo conduce a un sistema en donde el comportamiento de los portadores de carga está regido por la ecuación de Dirac-Weyl, la cual es una ecuación diferencial matricial propuesta en 1929 por Hermann Weyl para caracterizar el comportamiento relativista de partículas sin masa de espín ½.
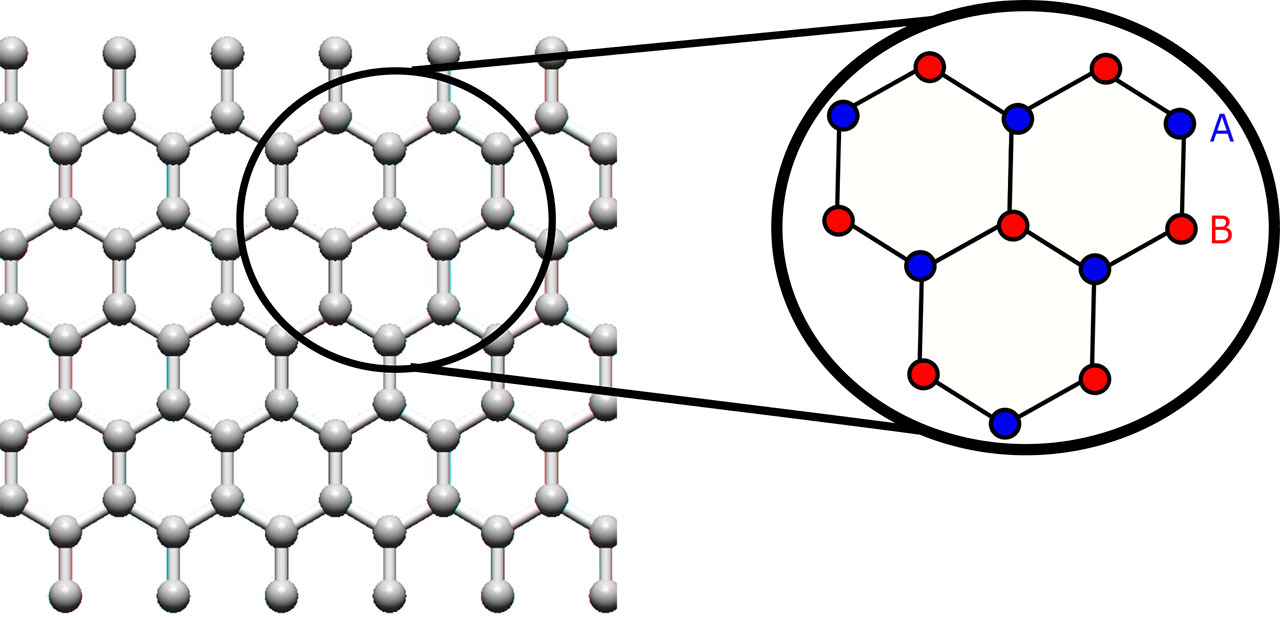
En el caso del grafeno, los portadores de carga se comportan como partículas cuánticas en una teoría de relatividad análoga en donde la velocidad de la luz es sustituida por la velocidad de Fermi 𝛖F, que es 300 veces menor que la velocidad de la luz en el vacío (𝛖F≈106 m/s), mientras que el espín caracteriza al grado de libertad que tienen los portadores de carga para estar en la subred A o B, lo que se denomina pseudo espín. Notemos que por teoría de la relatividad análoga nos referimos a sistema descritos por las mismas ecuaciones de la relatividad, pero con una connotación física distinta. La ecuación mencionada luce de la siguiente manera
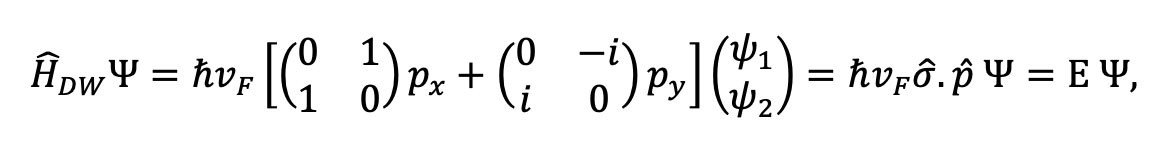
donde px y py son los momentos lineales en dirección x y y asociados a los portadores de carga, las componentes de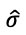 
se conocen como matrices de Pauli y Ψ es el vector columna solución a tal ecuación.
Comportamiento del grafeno en campos magnéticos
Las barreras electromagnéticas en el grafeno han permitido poner a prueba situaciones propias de la Mecánica Cuántica Relativista, como el tunelaje de Klein en donde un electrón relativista atraviesa una barrera sin sufrir dispersión alguna, o el efecto Hall en el cual la conductividad del material toma valores discretos. Con ciertos campos magnéticos aplicados al grafeno podemos confinar a los portadores de carga a una región espacial; una consecuencia cuántica de este confinamiento se traduce en que la energía de los portadores de carga deja de tomar valores continuos y solo son posibles algunos valores muy específicos. A este efecto se le conoce como cuantización de la energía y sucede, por ejemplo, al aplicar un campo magnético constante perpendicular a la hojuela de grafeno (Figura 3).
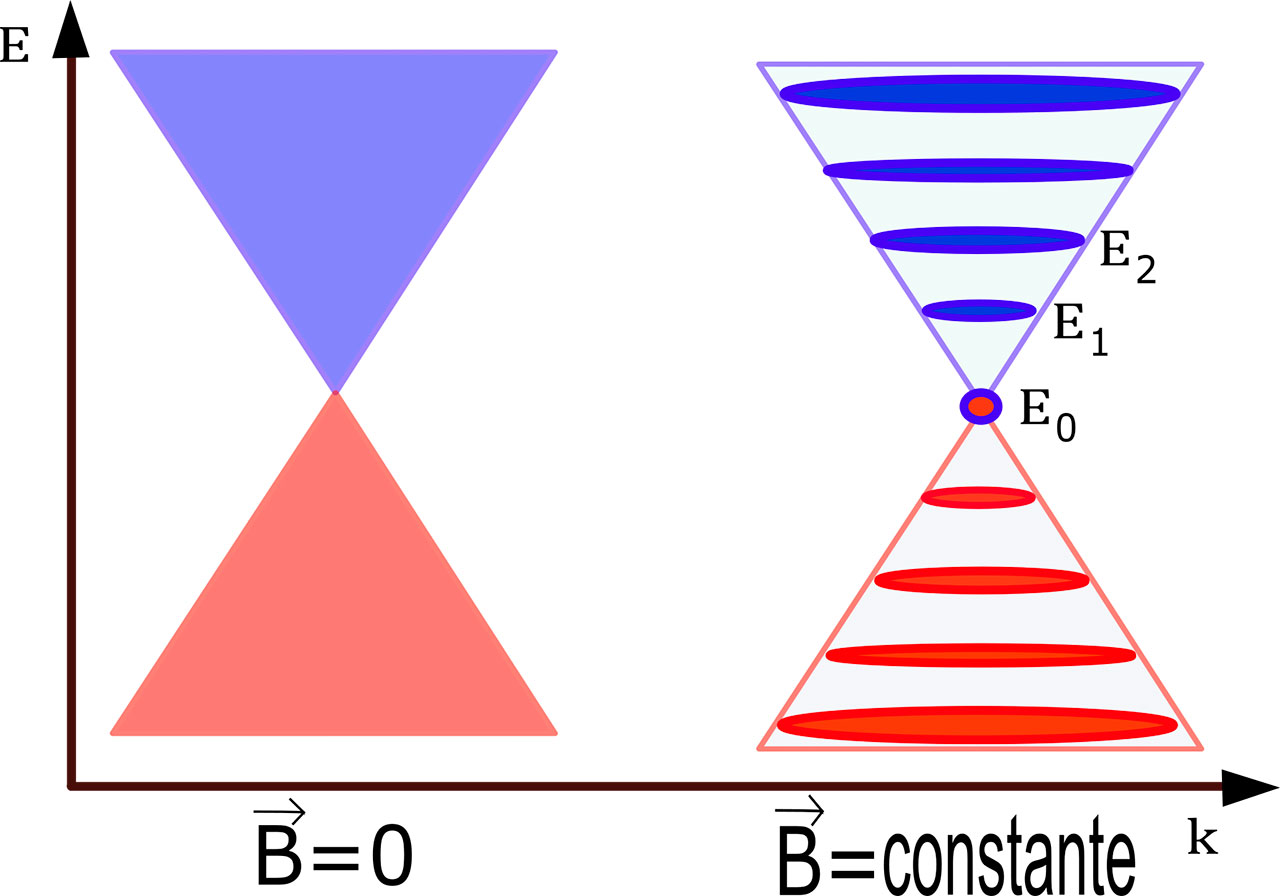
y niveles discretos de energía con campo magnético (derecha).
Para modelar matemáticamente a los portadores de carga del grafeno en un campo magnético externo, la ecuación de Dirac-Weyl se modifica de la siguiente manera:
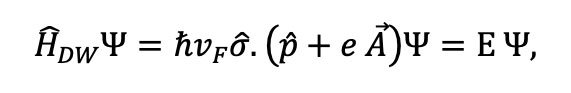
donde Ε es la energía del sistema, –e es la carga del electrón y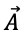 
se conoce como potencial vectorial, el cual está relacionado con el campo magnético externo mediante el operador rotacional en la forma 
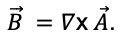Como se puede ver, solo se ha sumado un término al momento en la ecuación de Dirac-Weyl manteniendo invariante su estructura, 
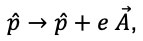lo cual se conoce como principio de acoplamiento mínimo.
La ecuación de eigenvalores por resolver es matricial, así que al desacoplar las componentes surgen dos ecuaciones cuadráticas en el momento análogas a la ecuación de Schrӧdinger que aparece típicamente en Mecánica Cuántica no Relativista. Esquemáticamente se tiene que:
Las energías potenciales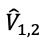 
dependen del potencial vectorial 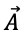. Por conveniencia nos podemos limitar a estudiar perfiles de campo magnético que conducen a ecuaciones de Schrӧdinger 
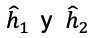y con solución analítica. Una elección típica consiste en escogerlo con una sola componente y que sólo varie en la dirección “x ” o “y”, con la finalidad de que las ecuaciones que surjan se puedan desacoplar.
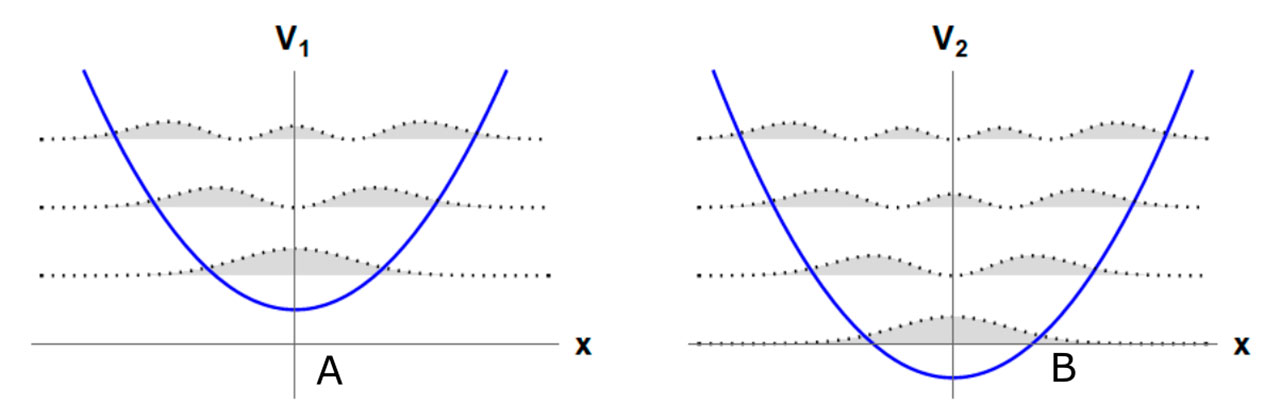
Los potenciales para los que la ecuación de Schrӧdinger se puede resolver de manera exacta fueron analizados de modo muy completo en 1951 por Infeld y Hull [2]. Los potenciales de ese trabajo se conocen actualmente como potenciales invariantes de forma, ya que se puede obtener uno a partir del otro mediante un cambio de los parámetros y un desplazamiento en la energía. Por ejemplo, en el caso del campo magnético constante aparecen dos ecuaciones de Schrӧdinger, cuyos potenciales corresponden al oscilador armónico (Figura 4).
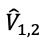
En 1984 Bogdan Mielnik, profesor del Departamento de Física del Cinvestav, hizo una contribución muy relevante al método de factorización de Infeld y Hull, la cual permitió extender el método a potenciales NO invariantes de forma [3]. Con el tiempo, esta técnica también ha sido conocida como Mecánica Cuántica Supersimétrica o SUSY. Sus aplicaciones van desde aspectos teóricos de la mecánica cuántica no relativista y relativista hasta temas más experimentales en sistemas ópticos o de estado sólido.
Los Hamiltonianos de Schrödinger son operadores de segundo orden en sus derivadas. Si dos de ellos,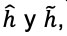 
, se pueden factorizar en operadores diferenciales de primer orden, llamémosles 
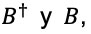de tal forma que 
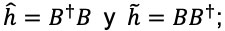la solución a la ecuación de Schrödinger se simplifica considerablemente o permite obtener más información. A esta manera de resolverla se le conoce como método de factorización, el cual es similar a la factorización de una ecuación cuadrática del tipo 
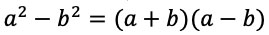pero teniendo en cuenta que en el caso cuántico se debe respetar el orden de los factores. Estos Hamiltonianos 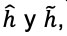son conocidos como socios supersimétricos.
En el caso del grafeno, el desarrollo adecuado del método de Mielnik sugiere tomar inicialmente un sistema de Dirac-Weyl que se relacione con dos potenciales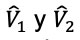 
que sean invariantes de forma. Posteriormente se debe escoger uno de esos dos potenciales para aplicar la técnica. Este procedimiento se puede interpretar como una máquina, la Máquina de Mielnik, a la cual se le introduce un potencial seleccionado 
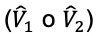para obtener como resultado dos potenciales no invariantes de forma (Figura 5):
Al acoplar apropiadamente el par de potenciales no invariantes de forma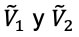 
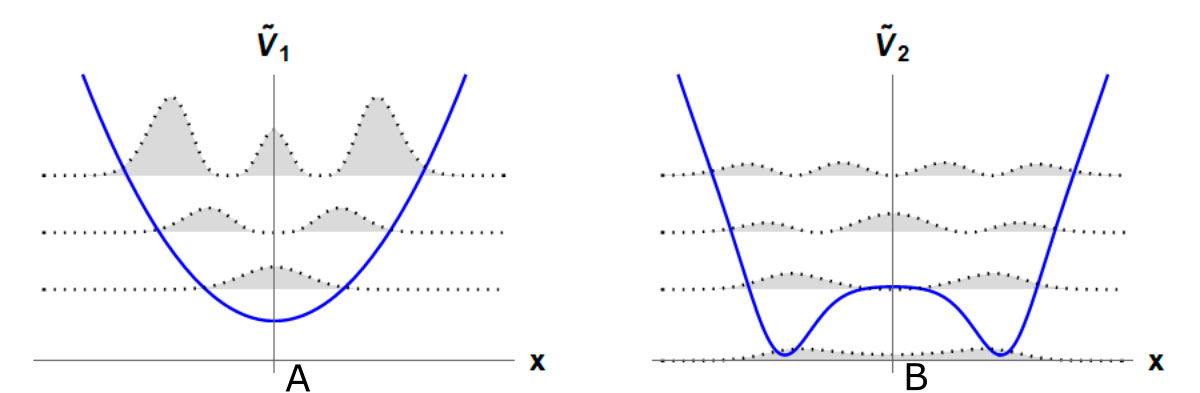
se obtiene una nueva ecuación de Dirac-Weyl (denotada en la Figura 5 por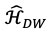 
), cuyo campo magnético asociado muestra una modificación concentrada en las zonas donde el potencial que rompe la invariancia de forma se modifica sustancialmente con respecto al inicial, aunque asintóticamente ambos potenciales son similares. En nuestra investigación hemos detectado que las irregularidades del nuevo campo magnético externo producen un cambio en los niveles de energía del sistema inicial debido a la introducción de un nuevo valor discreto en las energías posibles. Así, para el campo magnético inicialmente constante, el método de Mielnik produce un campo distorsionado, el cual tiene asociado dos potenciales como los que se observan en la Figura 6, en donde se ve claramente que se ha deformado una de las dos parábolas del oscilador armónico inicial (comparar con Figura 4).
En este ejemplo, el campo magnético constante, que en una gráfica de campo en función de posición, se representa por una línea horizontal, pasa a tener una modificación como se observa en la Figura 7a, donde en rojo hemos representado un campo magnético constante, y en azul a uno variable con modificaciones considerables entre -6 y 2 que asintóticamente tiende al campo constante. Este campo se ha conseguido usando la máquina de Mielnik y por ello es posible su descripción matemática exacta. En la Figura 7b, se ilustra también la forma en que se modifican los niveles de energía debido a la deformación del campo magnético.
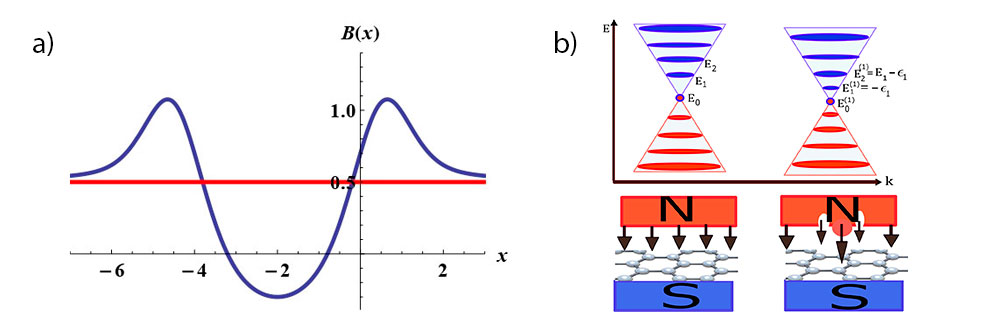
comparado con el campo constante inicial (línea roja). (b) Niveles
de energía para el sistema con campo constante y con campo modificado.
Lo anterior ha inspirado a diversos físicos teóricos a analizar distintos perfiles de campo magnético que puedan confinar a los electrones para discretizar los niveles de energía, creando así espectros discretos distintos al generado por un campo constante.
El grupo de Gravitación y Física Matemática del Departamento de Física del Cinvestav, en una amplia colaboración con profesores de la Universidad Michoacana de San Nicolás de Hidalgo, el Instituto Politécnico Nacional y la Universidad Nacional Autónoma de México, se ha interesado en explicar lo que pasa cuando se modifica el campo electromagnético aplicado a una monocapa o a una bicapa de grafeno, la forma en que cambian sus propiedades de transporte y las implicaciones que conlleva resolver teóricamente este tipo de sistemas. Además, ha sido pionero en el estudio de los estados coherentes del grafeno, que consiste en determinar las combinaciones lineales adecuadas de los estados propios de la energía para representar los estados más clásicos posibles.
Para concluir, queremos resaltar que las aplicaciones del método de factorización aquí descritas han sido inspiradas por el bagaje cultural que los fundadores del Departamento de Física de Cinvestav le heredaron a los autores de esta nota, ver por ejemplo [4].
Referencias
[1] Wallace, P. R. (1947). The band theory of graphite. Physical Review, 71(9), 622.
[2] Infeld, L., & Hull, T. E. (1951). The factorization method. Reviews of Modern Physics, 23(1), 21.
[3] Mielnik, B. (1984). Factorization method and new potentials with the oscillator spectrum. Journal of Mathematical Physics, 25(12), 3387-3389.
[4] Mielnik, B. (2016). Visiones incompletas… Avance y Perspectiva, 1(4), 8 (Una versión en inglés de este artículo se puede ver en Geometric Methods in Physics XXXIX, Trends in mathematics, P Kielanowski et al Eds., Birkhäuser, Springer Nature, Switzerland A.G, pp. 9-18 (2023)).
Foto de portada: rawpixel.com