En Apología de un Matemático, Godfrey H. Hardy expuso, entre otras cosas, sus convicciones personales acerca de la estética de las matemáticas. En su opinión, la belleza de un resultado matemático tiene mucho que ver con lo que llama su “seriedad”. De acuerdo con Hardy, la demostración de Euclides de la existencia de una cantidad infinita de números primos es un ejemplo paradigmático de un teorema “serio”, pues es corta, simple y significativa, entendiendo esto como la capacidad del teorema de conectar de una manera natural e iluminadora muchas áreas de las matemáticas. Para Hardy, un resultado significativo debe poseer dosis adecuadas de generalidad y profundidad. Sin estos ingredientes, un teorema no pasará de ser una mera curiosidad matemática y será completamente intrascendente, por más ingenioso que sea.
Extrapolando las ideas de Hardy al campo de la física, puede argumentarse que las ecuaciones de Maxwell son excelente ejemplo de un resultado “serio”. En ellas, James Clerk Maxwell resumió de forma por demás elegante leyes cuantitativas (formuladas desde finales del siglo XVIII) que relacionaban las interacciones entre los campos eléctricos y magnéticos, así como las corrientes eléctricas. Se trata de las leyes de Gauss, Faraday-Lenz y Ampere, esta última generalizada por el propio Maxwell. La síntesis de éste permitió unificar conceptualmente a la electricidad y el magnetismo, y dio pie a la búsqueda (continuada hasta nuestros días) de la teoría de la gran unificación y de la teoría del todo. Más aún, las ecuaciones de Maxwell tuvieron un impacto profundo en el desarrollo del cálculo vectorial, la teoría de la relatividad y la electrodinámica cuántica.
Para satisfacer el principio de conservación de la carga eléctrica, Maxwell incluyó un término adicional (relacionado con la llamada corriente de desplazamiento) en la ley de Ampere. Con esta modificación, las ecuaciones de Maxwell predijeron la existencia de ondas electromagnéticas que se propagan a la velocidad de la luz: ello permitió identificar a la luz como una onda electromagnética y unificar a la óptica con el electromagnetismo. Pero había un problema. De acuerdo con las ecuaciones de Maxwell, la velocidad de las ondas electromagnéticas era independiente de la velocidad del observador, con lo que el electromagnetismo entraba en contradicción con la mecánica clásica de Newton.
Hendrik Antoon Lorentz estudió la inconsistencia entre el electromagnetismo y la mecánica clásica. Descubrió en 1900 que (al cambiar de sistema de referencia) las ecuaciones de Maxwell no son invariantes ante las transformaciones de Galileo (como son las leyes de Newton), sino ante otro conjunto de transformaciones que ahora llevan su nombre. Esto iba al corazón de la física de principios del siglo XX, pues desde Newton se acepta que las leyes del universo deben de ser independientes del punto de referencia del observador.
Al igual que sus contemporáneos, Lorentz pensaba que la invariancia de la velocidad de transmisión de las ondas electromagnéticas evidenciaba la existencia de un sistema de referencia privilegiado (el éter). Sin embargo, Albert Einstein tuvo la audacia de asumir que las transformaciones de Lorentz eran correctas en un espacio-tiempo tetradimensional y en consecuencia, había que modificar las leyes de la mecánica. Con ello, dio lugar a la teoría especial de la relatividad.
Aunado a los ejemplos anteriores, las ecuaciones de Maxwell dieron lugar a otro problema que no es tan conocido, pero que ha impactado diversos campos de la física. Una de las predicciones del electromagnetismo es que una partícula cargada acelerada emite radiación, lo que a su vez implica una pérdida de energía que debe impactar el estado de movimiento de una partícula, de forma análoga al culatazo que sufre un arma de fuego al ser disparada. A este fenómeno se le conoce como reacción a la radiación.
A principios del siglo XX, Max Abraham y, en forma independiente, Lorentz, estudiaron la reacción a la radiación, llegando al siguiente resultado mediante consideraciones similares acerca de la estructura del electrón (descubierto por Thompson en 1897) y las interacciones entre sus partes:
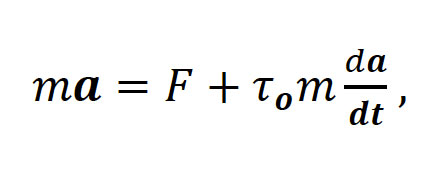
donde a, F y τo = (2/3) e2/mc3 representan la aceleración, la fuerza aplicada y el tiempo característico del electrón, respectivamente. Como puede apreciarse, la ecuación corresponde a la segunda ley de Newton, más un término adicional conocido como fuerza de Abraham-Lorentz o fuerza de reacción a la radiación. Numerosos físicos han abordado este problema, empleando diversas consideraciones, llegando a resultados equivalentes, cuya validez se ha verificado experimentalmente en el régimen de bajas velocidades en determinadas circunstancias físicas.
A pesar de todas sus virtudes, la fuerza de Abraham-Lorentz no está exenta de problemas físicos conceptuales:
- Es posible asociar una energía (autoenergía) con la fuerza de Abraham-Lorentz, que depende del tamaño de la partícula cargada. Si como se sospecha, el electrón es una partícula puntual, entonces la ecuación de Abraham-Lorentz predice que su autoenergía diverge, lo que no puede suceder. Para solucionar este problema, Dirac propuso su famosa renormalización, que fue pieza fundamental en el desarrollo de la electrodinámica cuántica.
- La ecuación de Abraham-Lorentz admite algunas soluciones no físicas. Por ejemplo, si la fuerza es cero, la aceleración crecerá exponencialmente con el tiempo, lo que contradice la primera ley de Newton. De acuerdo con Dirac, para resolver este problema es necesario invocar un principio adicional que obliga a considerar una aceleración inicial nula.
- Otro problema surge cuando se supone que la fuerza es nula hasta cierto momento, y crece abruptamente. La solución en este caso predice que la aceleración aumenta exponencialmente hasta el momento en que aparece la fuerza, y a partir de ese momento toma un valor constante, consistente con la segunda ley de Newton. En otras palabras, la partícula se acelera desde antes de que aparezca la fuerza que actúa sobre ella, violando el principio de causalidad (ver Fig.1). Para resolver el problema, Dirac mostró que la pre-aceleración ocurre a lo largo de un periodo del orden del tiempo característico τo (6.26×10-24 s para el electrón), en el que la física clásica ya no es válida.
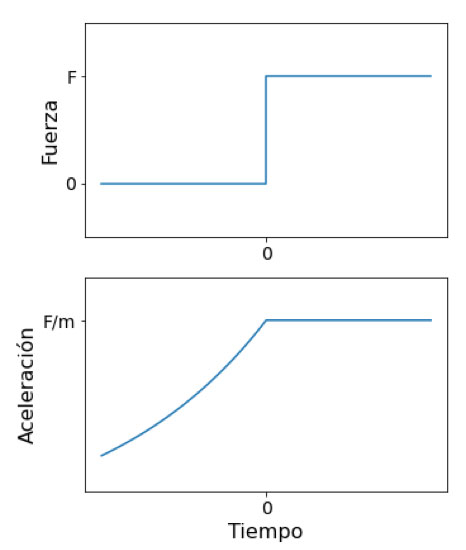
- Cuando la fuerza aplicada es constante, la solución de la ecuación de Abraham-Lorentz predice una aceleración constante, como si la emisión de radiación no afectase el movimiento de la partícula. Este problema, conocido como la paradoja del campo constante, requiere de consideraciones relativistas para ser explicado.
La fuerza de Abraham-Lorentz originó diversos problemas físicos fundamentales, y para solucionarlos fue necesario echar mano de la teoría de la relatividad y la mecánica cuántica. Al abordar el problema, Dirac generalizó la ecuación de Abraham-Lorentz al caso relativista, dando lugar a la ecuación conocida como de Abraham-Lorentz-Dirac (ADL). Posteriormente, Richard Feynman y John A. Wheeler, motivados por los comentarios de Dirac, volvieron a encontrar la ecuación ALD, haciendo uso de una teoría de acción a distancia, así como la famosa suposición del absorbedor perfecto. Estas herramientas y las ideas de la renormalización de la masa llevaron más tarde a Feynman a desarrollar la electrodinámica cuántica.
El problema parecía cerrado hacia mediados del siglo pasado, pues todas las inconsistencias físicas de la ecuación ALD se podían atribuir a efectos cuánticos. Sin embargo, Dirac mismo había dicho que la ecuación debe de ser capaz de describir correctamente fenómenos dentro de los límites de la electrodinámica clásica. La búsqueda de una expresión para la fuerza de reacción a la radiación, que carezca de inconvenientes físicos en el régimen clásico, ha atraído a no pocos científicos renombrados. Por mencionar a algunos: Eliezer, Landau, Lifshitz, Sphon, Rohrlich, Ford, O’Connell, Krivinskii y Tsytovich. No existe aún respuesta definitiva, aunque parece haber consenso de que la ecuación de Ford:
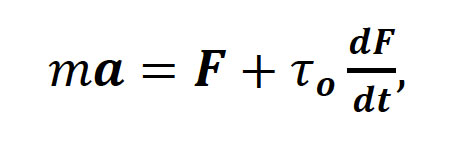 (2)
(2)
ofrece una descripción adecuada en el límite no relativista. Al extenderse al límite relativista, la ecuación es compatible con la de Landau y Lifshitz.
En años recientes se ha desarrollado la tecnología necesaria para producir pulsos electromagnéticos con ultra altas intensidades (del orden de 1022W/cm2). Esto ha permitido realizar experimentos encaminados a determinar cuál es la ecuación de movimiento que mejor modela la reacción a la radiación. Los resultados obtenidos a la fecha apuntan a que la ecuación de Landau y Lifshitz es la que describe el movimiento de una partícula cargada sin espín, dentro los límites de la electrodinámica clásica.