Después de casi un año de que apareció la Covid-19 en nuestras vidas, hay muchas discusiones acerca del manejo de la pandemia en distintos países y también entre diferentes comunidades. Este debate es importante, por ejemplo, para saber si es necesario poner mayor atención en zonas específicas de una ciudad, en determinadas regiones de un país, o incluso para saber cómo se desarrolla la pandemia en un país determinado.
Existen muchas formas de hacer estas valoraciones, que pueden ser difíciles de entender por el común de la población. La evaluación comparativa posiblemente de lugar a un desvío de la discusión hacia temas que van más allá del objetivo de la comparación, tomada como herramienta para evaluar la situación de una zona determinada.
El problema de presentar una forma simple, útil y entendible demanda que se defina un solo parámetro para hacer la evaluación; y que esta cantidad transmita de manera sencilla la situación de la zona donde vivimos, comparada con el resto. Esta tarea se complica si consideramos, además, que incluir ciudades o países que lo hacen ‘mejor’ lleva muchas veces al recelo natural de pensar que dicha región tenga condiciones distintas. Pensemos en el ejercicio simple de poner una ‘calificación’ y asignar, por ejemplo, un 10 al diez por ciento de países con menos contagios y un cero al diez por ciento en la situación opuesta. Inmediatamente se tendrá una discusión centrada más en ‘qué país es mejor’, ‘quién está al lado’, en lugar de centrarse en ‘cómo mejorar nuestra situación’.
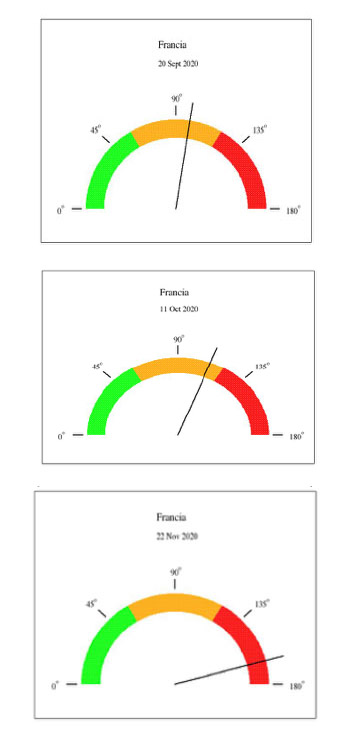
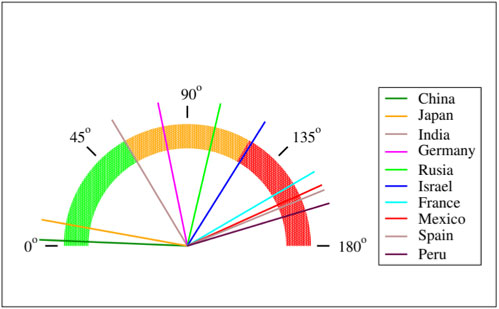
A manera de ejemplo mostramos la evaluación de Francia en tres semanas diferentes utilizando el parámetro aquí descrito. Se comparan los decesos en Francia en una semana con los decesos totales en el mundo en el mismo periodo, tomando en cuenta la población de Francia y del globo.
Tomando estos lineamientos como guía, se presenta aquí una forma simple de hacer esta evaluación y dos formas de mostrarla de manera entendible a un público amplio. Las ideas expuestas son sencillas y la herramienta matemática necesaria debe ser entendible por un alumno avanzado de educación preparatoria, mientras que la presentación de resultados permite a cualquier persona entender, de un vistazo, como se encuentra su entorno en comparación con el resto.
Posiblemente este tipo de análisis ya exista dado la sencillez de los mismos; se exponen como un ejercicio más para entender cómo se está comportando la pandemia en cada región y también como una práctica interesante para reforzar conceptos matemáticos básicos de trigonometría.
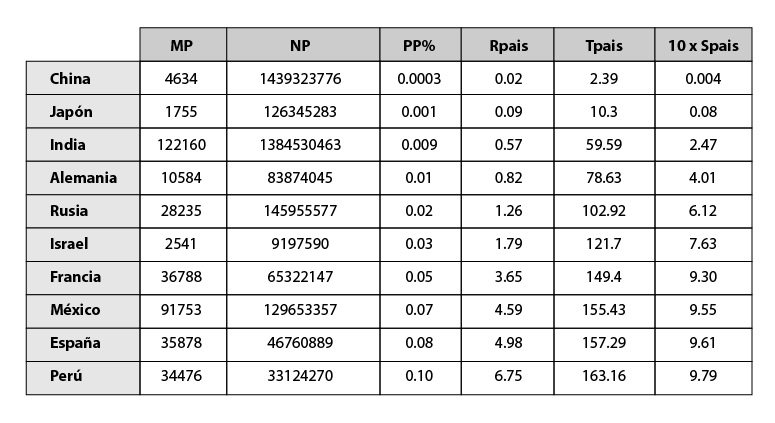
Hay en el mundo un poco más de 220 países. A cada uno de ellos la pandemia lo ha afectado en mayor o menor grado. Considerando que la población mundial es aproximadamente de siete mil millones de habitantes, se puede calcular el porcentaje de fallecidos por la Covid-19 en el mundo: llamémosle PT. Por otro lado, para cada país podemos obtener también el porcentaje de fallecidos respecto a su población (PP). Es sencillo concluir que los países con una tasa porcentual mayor al porcentaje mundial lo están haciendo un poco peor, o incluso mucho peor si se alejan demasiado de este valor mundial. Hasta aquí, se necesitan al menos dos cantidades para comprender qué tan bien o mal está un país respecto al mundo. Además, puede ser difícil tener una idea de qué tan mal (o qué tan bien) se está, al no tener una idea de lo que representan estas desviaciones entre los dos números en cuestión.
Se toma el cociente del porcentaje de muertes en un país y el de muertes en el orbe para tener un solo número que nos dé una idea rápida de cómo está el país o región bajo estudio. Así, la desviación respecto al promedio mundial la podemos definir como la razón (Rpais) entre estas dos cantidades: PP entre PT.
Esto implica que un país con un comportamiento promedio tendrá asignado un valor igual a uno, los que están por debajo del promedio serán menores a uno y los que están por arriba del promedio tendrán un valor mayor a uno. De esta manera se tiene un único parámetro para describir la situación de un país o región, pero aún subsiste el problema de entender fácilmente el significado del valor concreto. Es cierto que se buscaría estar por debajo del valor de uno, pero es todavía difícil entender que significaría un valor de 5 o de 15, cuando estamos por encima del promedio. Y es que el problema en esta cantidad es la dificultad de definir un límite superior a esta proporción.
Para solucionar este problema podemos recurrir a las funciones trigonométricas y obtener así un parámetro acotado que no crezca indefinidamente. Una vez que se acota el rango de variación el parámetro sería ajustable y se podría poner en una escala, por ejemplo, de cero a ciento ochenta grados, donde noventa grados sería el valor que coincide con el promedio mundial. Antes de ver cómo obtenerlo, observemos que el parámetro Rpais se puede ajustar fácilmente a un estado o región. Se podría, además, definir como parámetro de comparación el promedio mundial, o bien el promedio de un país para comparar cómo se comporta cada región con respecto al promedio del país. También podríamos dar una ‘calificación’ opuesta (el país que está por debajo del promedio tendría un valor mayor que uno) tomando el inverso de Rpais, es decir 1/Rpais. Finalmente, no está por demás comentar que se puede usar el porcentaje de muertes o también el número de muertes por millón de habitantes, que da exactamente el mismo resultado.
Veamos ahora como acotar el problema usando funciones trigonométricas. Para ello podemos tomar la tangente inversa de Rpais; es decir, buscar el ángulo para el cual su tangente es precisamente Rpais. De la trigonometría básica, sabemos que la tangente de cero es cero, la tangente de cuarenta y cinco grados es uno y la tangente de noventa grados es igual a infinito. Así que cualquier valor de Rpais (incluso infinito) estará contenido en el rango de cero a noventa, siendo cuarenta y cinco el valor que coincide con el promedio mundial y con Rpais igual a uno.
Ahora solo nos falta poner un rango de valores que pueda expresarse de manera gráfica y nos informe nuestra situación de manera sencilla. Esto podrá obtenerse mediante el seno del ángulo elevado al cuadrado. Haciendo esta operación, el valor central será precisamente un medio, el valor mínimo, cero y el peor escenario nos dará uno. Si en lugar del seno se utiliza la función trigonométrica coseno se obtendrá una escala invertida, donde uno es el mejor escenario y cero el peor.
Una forma de evitar el uso de esta segunda transformación trigonométrica (el uso del coseno o del seno) sería simplemente multiplicar el ángulo por dos y así tener una escala de cero a ciento ochenta grados que se puede graficar en un semicírculo, muy parecido a un velocímetro. En este caso, si la manecilla está a la mitad, el país o región bajo estudio se encuentra en una situación normal respecto al resto de la muestra, mientras que si está en un valor mayor (hacia la derecha si lo graficamos como velocímetro) habrá que tomar medidas para mejorar. Podrían definirse tres regiones para saber en qué rango se encuentra el país o comunidad: de cero a sesenta grados sería una zona confortable por debajo del porcentaje global, de sesenta a ciento veinte se estaría en una zona intermedia, comparable con el desempeño promedio, y finalmente de ciento veinte a ciento ochenta grados se estaría en un desempeño que necesita mejorarse.
Exponemos a continuación la descripción de la discusión que hemos desarrollado.
En una fecha determinada (tomamos el 1 de noviembre, como ejemplo), se reportan en el mundo un total, MT, de muertes (de acuerdo con la página de internet https://www.worldometers.info/coronavirus/).
Indicamos el número de fallecidos, en un determinado periodo y región, como MP y a la misma cantidad, pero para la muestra total (el mundo o la región completa de estudio) como MT. Abreviamos la población del país como NP y la mundial como NT. Partimos entonces de considerar el porcentaje mundial PT = 100 x MT / NT, es decir
PT = 100 x (muertes en el planeta) / (población mundial)
y al porcentaje de muertes en un país PP = (100 x MP)/ NP como
PP = 100 x (muertes en un país) / (población del país)
La desviación respecto del promedio mundial la podemos medir como la razón o división de estas dos cantidades:
Rpais = PP / PT
A partir de esta cantidad, podemos pasar a un parámetro acotado entre 0 y 180 grados, tomando la tangente inversa (conocida también como arctan) de Rpais y multiplicándola por dos:
Tpais = 2 x arctan(Rpais)
Si quisiéramos además ajustar esta cantidad a una región entre cero y uno podríamos utilizar la función seno:
Spais = [ sen( Tpais / 2 ) ]^2
y para tener un rango que vaya justo en sentido opuesto se puede utilizar el coseno en lugar del seno.
Para hacer la figura 1 se tomó en cuenta la población de Francia reportada en https://www.worldometers.info/coronavirus y una población mundial de siete mil millones de habitantes. Se tomaron los reportes semanales de fallecidos de la Organización Mundial de Salud (OMS) de los días 20 de septiembre,11 de octubre y 22 de noviembre. Esta información se presenta en la siguiente tabla.
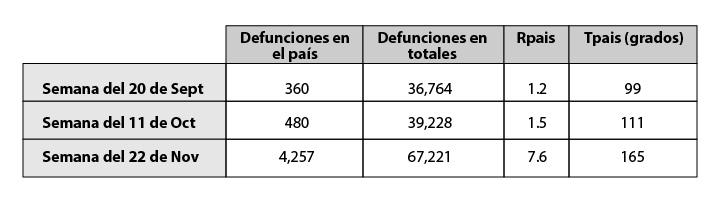
Para elaborar la figura 2 de este escrito se utilizaron los datos que se muestran en la siguiente tabla y que dan la medición utilizando los distintos parámetros aquí enunciados. Todos los datos de la tabla siguiente fueron tomados de la página https://www.worldometers.info/coronavirus al día 1 de noviembre.