Hoy en día existen algunos fenómenos físicos que apenas estamos entendiendo o aprovechando. Un ejemplo son los materiales topológicos, que corresponden a una combinación no trivial de aislante y conductor en el mismo material. Sería de gran utilidad estudiar estos sistemas de manera controlada en un laboratorio, pero ¿cómo? La respuesta podría surgir de un campo en la frontera de la investigación científica que se conoce como campos de norma artificiales o artificial gauge fields por su nombre en inglés.
En física, una teoría de norma es un tipo de teoría de campos en la cual existen simetrías especiales; en particular, las ecuaciones que describen a los campos permanecen invariantes ante ciertas operaciones. Una teoría de norma muy conocida es el electromagnetismo, en la que los campos eléctrico y magnético se pueden definir matemáticamente en términos de campos de norma, lo cual facilita su descripción. Pero, ¿es posible crear un campo de norma artificial que actúe sobre una partícula de carga neutra?
Pues bien, ésta es la historia de un átomo (neutro) que un día se vistió de electrón. A continuación veremos cómo los átomos con carga neta igual a cero pueden conducirse de manera equivalente a partículas cargadas eléctricamente. Este comportamiento resulta de gran utilidad para entender sistemas de electrones. Como sabemos, los electrones en movimiento son responsables de la corriente disponible en todas las tomas eléctricas de nuestros hogares, que fluye por los electrodomésticos, incluidos los teléfonos celulares, computadoras, televisores, etcétera. Los átomos son objetos compuestos hechos de otras partículas que son al protón, neutrón y electrón, y aunque algunas de éstas poseen carga eléctrica, el átomo tiene una carga total igual a cero. Los electrones y los átomos son por lo tanto partículas muy distintas, ¿cómo puede una comportarse como la otra? y ¿qué ganaríamos con este logro?
La respuesta viene del lenguaje matemático de la naturaleza: existen fenómenos físicos cuyas leyes de movimiento tienen la misma estructura matemática que otros fenómenos, pero con variables muy diferentes. Como ejemplo el siguiente ejercicio: encuentre las similitudes de las siguientes ecuaciones
![]()
Una ecuación describe el movimiento de una partícula con carga eléctrica q y velocidad v inmersa en un campo magnético B; mientras que la otra describe el movimiento de una partícula de masa M con velocidad v sujeta a una rotación con velocidad angular Ω. Como cultura general, la primera ecuación se conoce como la fuerza de Lorentz y la segunda como la fuerza de Coriolis.
Lo importante es que “las mismas ecuaciones tienen las mismas soluciones”. Sólo que la solución en un caso representa una corriente eléctrica qv, mientras que en el otro corresponde a una corriente de partículas Mv. Y sí, una respuesta a nuestro problema — el vestir al átomo neutro como electrón por si ya lo habías olvidado,— es poner a los átomos neutros en rotación, ¡y funciona! como lo demostraron inicialmente los grupos de investigación de E. Cornell [1], J. Dalibard [2], y W. Ketterle [3]. Sin embargo, existe otra solución aún más generalizada que tiene que ver con la creación del paisaje de energía potencial adecuado para los átomos: en lugar de utilizar las fuerzas presentes para conocer la evolución de un sistema —como en la mecánica Newtoniana—, basta con conocer la energía en este nuevo formalismo. Pero a diferencia de la fuerza, no tenemos mucha intuición sobre la energía.
La energía por lo regular depende de la posición y de la velocidad. Por ejemplo, un electrón tendrá una cierta energía cinética adecuada a su velocidad y una energía potencial debida a su distancia con respecto a un electrodo cargado negativamente. Esta energía depende de los campos eléctricos y magnéticos presentes. De manera similar, la energía de un átomo que se encuentra iluminado por un haz láser será diferente a la que tendría en otra posición donde esté a oscuras. Aprovechando esta idea podemos hacer que la energía varíe con la posición con cualquier dependencia deseada. Por otra parte, lograr que la energía dependa de la velocidad es algo más complicado, pero no imposible. Para esto podemos utilizar el efecto Doppler, mediante el cual un átomo en movimiento percibirá una frecuencia (energía) de la luz láser menor si viaja en la misma dirección (o mayor si viaja en la dirección opuesta al láser). Con este corrimiento en frecuencia podemos hacer que la luz se encuentre más cerca de estar en resonancia con el átomo, y por lo tanto que tenga una interacción más fuerte. De esta manera la energía del átomo dependerá de su velocidad.
Manos a la obra. En un experimento con átomos neutros podemos poner los campos externos necesarios para generar alguna dependencia deseada de la energía como función de la posición y la velocidad. En particular, si somos lo suficientemente ingeniosos, podemos implementar una dependencia que sea análoga a la que siente un electrón en presencia de un campo magnético (que el átomo neutro sienta algo como la fuerza de Lorentz). Si el campo magnético apunta en la dirección vertical, y el electrón se mueve en el plano horizontal, entonces el electrón comenzará a dar vueltas en círculos en dicho plano. El radio de los círculos será más pequeño conforme aumente el campo magnético aplicado.
Un experimento desarrollado por Y.-J. Lin y colaboradores, logró reproducir el mismo comportamiento utilizando átomos neutros en lugar de electrones [4]; en este experimento participó Karina Jiménez García, coautora de este escrito. Para enfatizar por qué esto es algo complicado, pensemos un segundo lo que queremos lograr. Quisiéramos poner al átomo a dar vueltas en círculos, independientemente de su posición, cual si se tratara del electrón antes mencionado en un campo magnético (ver Eq. 1a). En su arreglo utilizaron átomos neutros iluminados por un par de haces láser y en presencia de un campo magnético como se muestra en la Figura 1a. En particular, se usaron átomos de rubidio que aunque son neutros, tienen un momento dipolar magnético, es decir, funcionan como pequeños imanes. Estos imanes atómicos pueden apuntar en una dirección (digamos +z, o arriba), en la dirección opuesta (-z, o abajo), o no tener dipolo (en z). Llamamos a estos tres posibles estados m=+1, -1 y 0 respectivamente (niveles de energía de la Fig. 1b). Al aplicar un campo magnético (B) estos estados aumentan (ΔE), disminuyen o no cambian su energía dependiendo del valor de m debido al efecto Zeeman. Si el campo magnético varía con la posición, es decir, si tenemos un gradiente de campo magnético, podemos ejercer una fuerza sobre los átomos cuyo signo depende nuevamente de m.
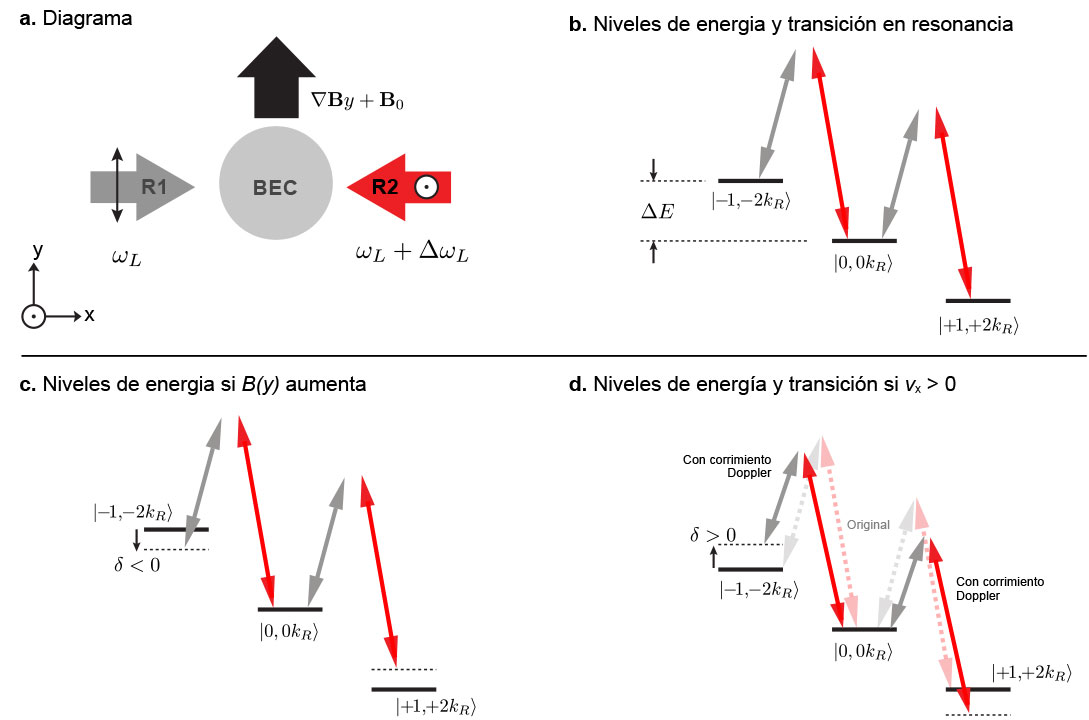
Podemos pasar de un estado m a otro mediante una transición de dos fotones (Raman) (flechas grises y rojas de la Fig. 1b). Si los dos láseres son contra-propagantes como en la Fig. 1a, dicha transición Raman imparte también momento lineal a los átomos (cada fotón imparte un momento p = Mv = h/λ donde h es la constante de Plank y λ la longitud de onda de los láseres). Esto conecta los grados de libertad internos del átomo (su m) con los externos (su velocidad v). Las frecuencias de los láseres se ajustan para que la diferencia de energía de sus fotones esté en resonancia con la separación de los niveles m, dado un campo magnético (Fig. 1b). Hay dos maneras equivalentes de sacar a la transición de resonancia (con una desintonía δ negativa). La primera se logra aumentando el campo magnético (Fig. 1c). La segunda se obtiene disminuyendo la velocidad del átomo, de manera que vean a los láseres con una frecuencia diferente debido al Efecto Doppler (Fig. 1d). El efecto de las dos es similar debido a la mezcla de grados de libertad antes mencionada.
La Figura 2 muestra la energía de los átomos, incluyendo su energía interna y su energía cinética (o de movimiento) cuando los láseres están apagados (líneas punteadas). Al prender los láseres, los niveles se acoplan entre sí, y operan de manera conjunta (línea rosa). Al incrementar la intensidad de los láseres (línea roja) la energía de cada átomo tiende a concentrarse en el mínimo de energía (punto rojo de la Fig. 2). Ya no hay una clara distinción entre los niveles m individuales, sino que los átomos se encuentran en un estado de superposición con diferentes amplitudes de los tres estados posibles:
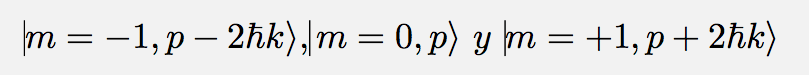
donde k = 2π/λ se conoce como el número de onda (ver Fig. 3).
El momento lineal de este nuevo sistema de átomos iluminados por luz es la media ponderada por la población en cada estado, y puede variar de manera continua y no sólo en brincos de Δp como lo hacen las componentes individuales. Algo parecido ocurre con el momento magnético del nuevo sistema, que ahora puede variar de manera continua.
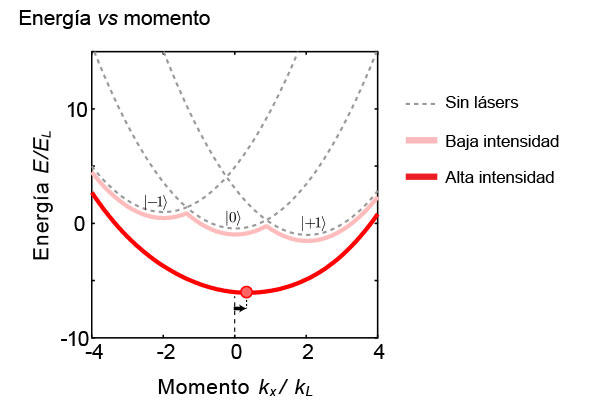
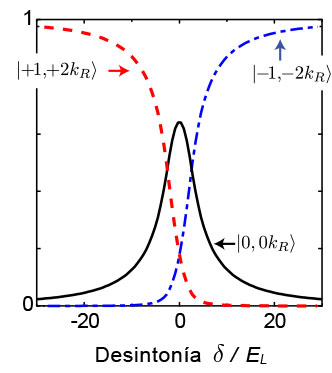
Si atrapamos una canica en el fondo de un tazón y lo movemos lentamente, la canica seguirá en el fondo del tazón, se moverá con él. De manera similar sucede aquí; si cambiamos la desintonía δ, causará que se mueva la curva roja de la Figura 2 (i.e. nuestro tazón), pero ahora en vez de corresponder a un cambio de posición, corresponde a una variación en la superposición de los tres estados, a un cambio del momento y a una redistribución de los estados m (Figura 3). El momento neto adquirido total en la dirección x (dirección en la que se propagan los lásers) es transferido de la luz a los átomos. Así es como este método logra generar potenciales dependientes de la velocidad, en lugar de la posición. De igual manera, la redistribución de los estados m combinada con el gradiente magnético introduce una fuerza en la dirección y.
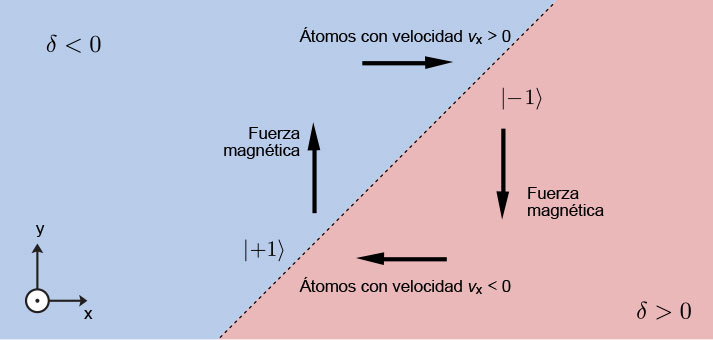
Dados los ingredientes anteriores podemos entender cómo surge el movimiento circular —propio de los electrones en un campo B y ahora imitado por átomos neutros— (Fig. 4):
- Empecemos con un átomo que se mueve en la dirección +y.
- Dada la dirección del gradiente, el campo B aumenta y δ decrece (Fig. 1c).
- En estas condiciones tenemos un cambio de momento neto positivo (Fig. 3) y los átomos se empiezan a mover hacia +x.
- Ahora el átomo se mueve en la dirección +x, su velocidad vx hace que δ se vuelva más positivo (Fig. 1d). Esta desintonía corre el mínimo de la Fig. 3 hacia kx < 0, por lo que la superposición tiene una mayor contribución del estado m=-1 (Fig. 3), lo cual, combinado con la fuerza que ejerce el gradiente de campo magnético resulta en una fuerza hacia -y.
- El átomo se mueve en la dirección –y y ocurre lo opuesto al inciso 1 lo cual empuja el átomo hacia –x.
- Al moverse en –x ocurre lo opuesto al inciso 4 y empuja al átomo hacia +y lo que cierra el ciclo y volvemos al inciso 1.
Y es así como un átomo neutro se vistió de electrón y experimentó una fuerza análoga a la fuerza de Lorentz. Este trabajo abrió una nueva área en la física llamada campos de norma artificiales. Son artificiales ya que aquí no se tiene un electrón, en su lugar se tiene un átomo. Tampoco existe en el experimento un campo magnético vertical; lo que se tiene es un gradiente de campo magnético y un par de láseres, que combinados crean un efecto similar sobre los átomos al que tendría un campo magnético sobre los electrones. El campo magnético artificial que se puede generar es órdenes de magnitud más grande que los campos magnéticos reales que se pueden formar hoy en día, lo cual permite, por ejemplo, el estudio de la física del efecto Hall cuantizado a campos magnéticos muy grandes.
Se llaman campos de norma ya que el énfasis aquí es simular la energía del sistema y no la fuerza como sería en el caso de Newton. A dicha energía se le puede aplicar una transformación particular, llamada transformación de norma, que lleva a una expresión diferente de la energía, pero que corresponde a exactamente la misma fuerza. Por ejemplo, podemos tener un sistema al cual le aplicamos una transformación de rotación, y nos encontramos que el comportamiento del sistema es idéntico ante dicha rotación. Gracias a esto podemos decir que el sistema es simétrico ante rotaciones. Describir a los sistemas en términos de campos de norma ha permitido en la física actual la introducción de conceptos de simetría en las leyes de la física. Mientras más simetrías tiene un sistema, más sencilla se vuelve su descripción.
Esta poderosa idea, que ahora ha sido llevada al laboratorio, permite la simulación de sistemas muy complejos mediante sistemas más simples sobre los cuales tenemos un gran control. Se espera que estos sistemas análogos puedan ayudarnos a entender mejor algunos de los fenómenos modernos y así poder explotarlos, como es el caso de los materiales topológicos.
REFERENCIAS
- M. R. Matthews, B. P. Anderson, P. C. Haljan, D. S. Hall, C. E. Wieman, and E. A. Cornell . Vortices in a Bose-Einstein Condensate. Phys. Rev. Lett. 83, 2498 (1999)
- K. W. Madison, F. Chevy, W. Wohlleben, and J. Dalibard. Phys. Rev. Lett. 84, 806 (2000).
- J. R. Abo-Shaeer et al. Observation of Vortex Lattices in Bose-Einstein Condensates. Science 292, 476 (2001). DOI: 10.1126/science.1060182
- Y.-J. Lin, R. L. Compton, K. Jiménez-García, J. V. Porto, and I. B. Spielman. Nature 462, 628-632 (2009).
Eduardo Gómez García1, Karina Jiménez García2
1Instituto de Física, UASLP, 2Cinvestav Querétaro