PREMIO ARTURO ROSENBLUETH de Ciencias Exactas y Naturales.
La física moderna tiene como piedras angulares a la mecánica cuántica y a la relatividad general. Gracias a la primera se ha logrado un conocimiento profundo de los constituyentes fundamentales de la materia, mientras que la segunda ha cambiado de manera notable nuestras nociones de espacio, tiempo y gravedad, dando una muy buena descripción del universo a gran escala.
Esta diferencia entre nuestras descripciones de lo muy pequeño y lo muy grande ha puesto en aprietos las bases mismas de la física, iniciando una incansable búsqueda por una descripción unificada y consistente de ambas teorías. Combinar de manera apropiada a la mecánica cuántica con la relatividad general se ha convertido en el principal reto de la física teórica moderna.
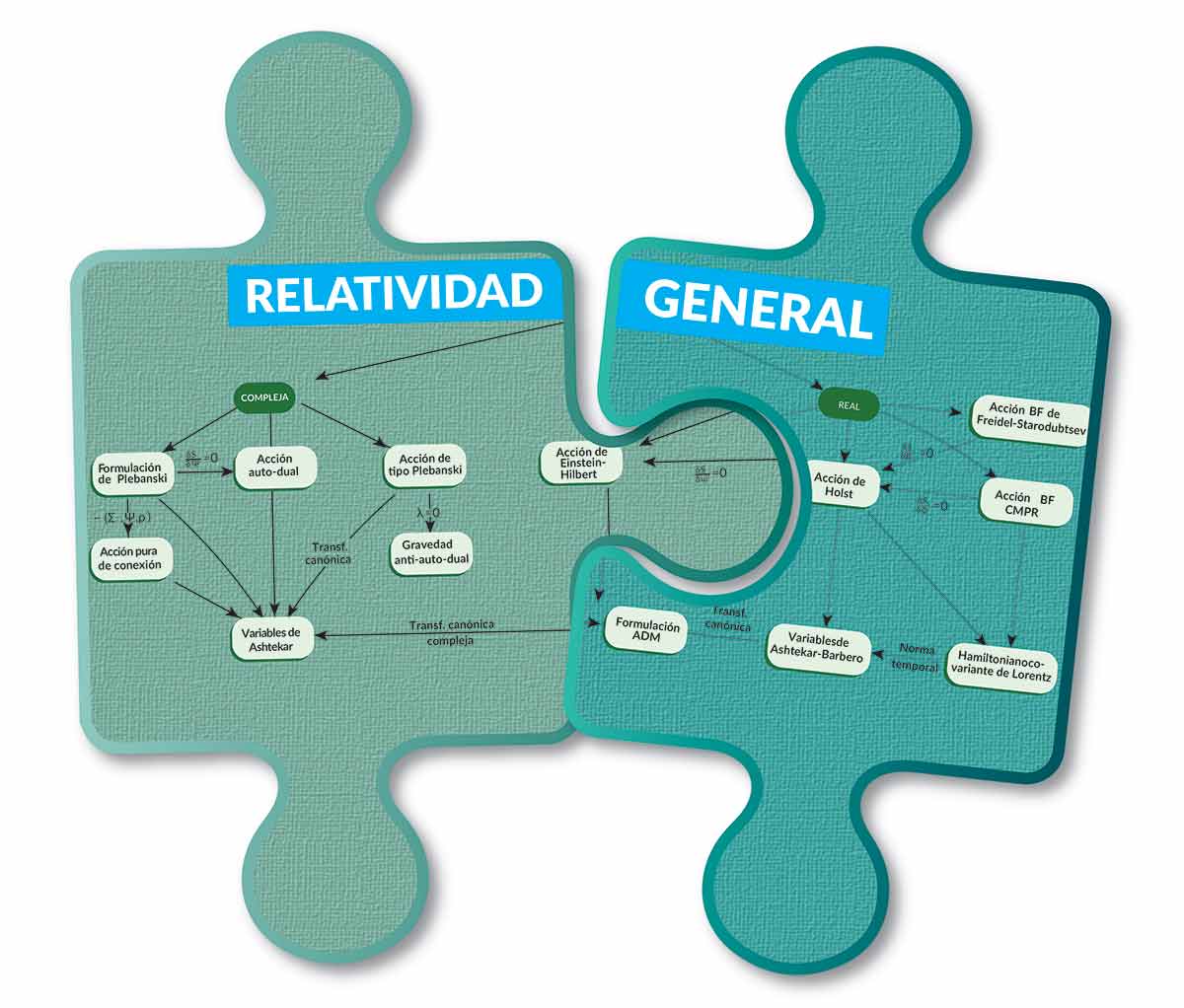
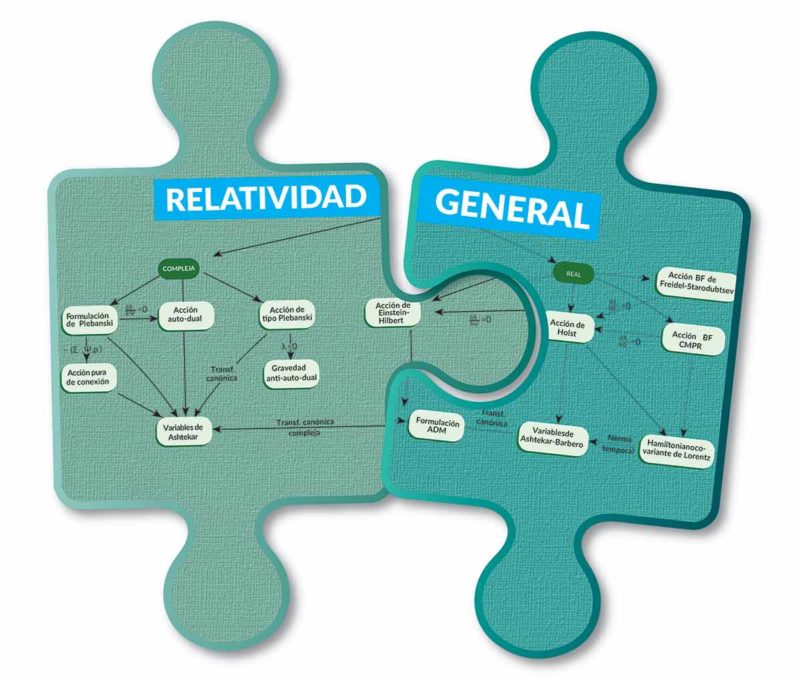
Entre los diferentes enfoques que buscan desarrollar una teoría cuántica de la gravedad, figuran aquellos que tratan de aplicar las reglas de la mecánica cuántica a la teoría de Einstein, lo que ha generado muchas ideas novedosas e interesantes, dos de las cuales son la gravedad cuántica de lazos y los modelos de espumas de espín. Ambos enfoques cuánticos de la gravedad tienen como punto de partida diferentes descripciones de la relatividad general y siguen distintos caminos. La gravedad cuántica de lazos toma como punto inicial la formulación de primer orden de la relatividad general dada por Holst, y sigue el programa de la cuantización canónica de Dirac, donde es necesario conocer la estructura del espacio de fase que posee la teoría (este método también es conocido como hamiltoniano).
Por otro lado, los modelos de espumas de espín parten de las formulaciones del tipo BF de la relatividad general, intentando a partir de ellas desarrollar una cuantización por integrales de camino (à la Feynman) de la misma. Los dos enfoques se complementan mutuamente y se han convertido en serios candidatos para la tan deseada descripción de la naturaleza cuántica de la gravedad.
Como las formulaciones del tipo BF de la relatividad general son en principio (clásicamente) equivalentes a aquellas de primer orden de la misma (como la de Holst), y dado que un conocimiento de la estructura hamiltoniana de las primeras es importante para establecer una conexión apropiada entre los resultados de los modelos de espumas de espín y los de gravedad cuántica de lazos, nos propusimos investigar la relación, a nivel hamiltoniano, de estas dos formulaciones de la relatividad general.
A partir de una formulación del tipo BF para la teoría de Einstein, que incluye el parámetro de Immirzi, una constante que juega un papel fundamental en la gravedad cuántica de lazos, obtuvimos la formulación de Ashtekar-Barbero. Dicha formulación es la que provee las variables con las cuales el enfoque de lazos construye todo su edificio teórico.
Así, las variables de Ashtekar-Barbero también emergen de las formulaciones del tipo BF de la relatividad general, algo que debe tenerse en cuenta a la hora de comparar los modelos cuánticos antes mencionados.
Sin embargo, nuestros resultados fueron más allá de establecer contacto con el enfoque canónico, ya que quisimos proveer nuevos puntos de vista que podrían jugar un papel relevante en posteriores desarrollos de la teoría cuántica de la gravedad. De esa manera, obtuvimos una formulación hamiltoniana de la relatividad general sin constricciones de segunda clase, que preserva la simetría de Lorentz (una simetría fundamental de la naturaleza), la cual está rota en la formulación de Ashtekar-Barbero. Esa nueva formulación podría dar nuevas ideas sobre el papel que juega tal simetría en la gravedad cuántica, además de ayudar a resolver los problemas conceptuales puestos por el parámetro de Immirzi en el enfoque canónico.
Las formulaciones del tipo BF de la relatividad general vieron su nacimiento con los trabajos de Plebanski. La acción homónima desarrollada por quien fuera investigador del Departamento de Física del Cinvestav, constituye la primera formulación del tipo BF o de 2-formas de la teoría de Einstein. Dado que las teorías BF puras tienen ciertas propiedades matemáticas atractivas, son apropiadas para explorar diferentes esquemas de cuantización, y como la relatividad general puede ser escrita en el marco de estas teorías, esos mismos esquemas tienen potencial de ser usados para aproximarse al problema de gravedad cuántica, dando lugar a los modelos de espumas de espín.
Otra parte de mi tesis doctoral estuvo dedicada al estudio de la acción de Plebanski y su relación con otras formulaciones de la relatividad general compleja, lo que nos permitió desarrollar un método sistemático y limpio que conecta la acción de Plebanski con una formulación pura de conexión de la relatividad general, mostrando que a nivel hamiltoniano dicha acción también conduce a las variables de Ashtekar.
Encontramos que la formulación pura de conexión emerge cuando uno elimina de la acción de Plebanski ciertas variables superfluas, pero a través de este procedimiento el carácter BF de la teoría se difumina. Fue así que propusimos un nuevo principio de acción similar al de Plebanski, pero con una dependencia funcional diferente en las mismas variables. Gracias a dicha dependencia, las diferentes variables involucradas podían eliminarse siguiendo diferentes caminos, llevando a una descripción de la relatividad general recientemente introducida donde esta teoría es vista como una teoría BF con un término de potencial que sólo depende del campo B. El nuevo principio permite además conectar la relatividad general y la gravedad anti-autodual, algo que no era posible a través de la acción de Plebanski.
Entre los resultados obtenidos con este trabajo, pudimos ampliar el conocimiento de las estructuras geométricas y físicas que subyacen a las formulaciones del tipo BF de la relatividad general, haciendo no sólo contacto con las estructuras conocidas en otras formulaciones de esta teoría, sino proponiendo nuevos puntos de vista útiles en la construcción de la teoría definitiva para describir apropiadamente las propiedades cuánticas del campo gravitacional. Sobra decir que aún falta mucho camino por recorrer para lograr tan anhelado objetivo, pero sin duda cada vez estamos más cerca de la edificación de un marco conceptual consistente donde la mecánica cuántica y la relatividad general se fundan en armonía.















12 comentarios
Visitor Rating: 5 Stars
Visitor Rating: 3 Stars
Visitor Rating: 2 Stars
Visitor Rating: 5 Stars
Visitor Rating: 5 Stars
Visitor Rating: 5 Stars
Visitor Rating: 1 Stars
Visitor Rating: 4 Stars
Visitor Rating: 5 Stars
Visitor Rating: 2 Stars
Visitor Rating: 3 Stars
Visitor Rating: 5 Stars
Comentarios no permitidos.