En un planeta lejano, la comunidad científica está amenazada y se persigue a cada científico que se opone al régimen galáctico. La emperatriz, Eileen, ha enviado a sus espías Alice y Bob a destruir la información de todos los científicos para que no se comuniquen ni colaboren. Idea su plan después de ver una luz azul en el cielo. Piensa en su espía Bob y le pide robar las listas que contienen la información para triturarlas y deshacerse de ellas. Sospechando que los residuos de las listas puedan reconstruirse, la emperatriz ordena a su espía Alice que destruya los restos en una trituradora idéntica a la de Bob (Figura 1). Sin embargo, Eileen medita y se da cuenta que el destello de luz que detonó su idea ha sido causal; si hubiese sido roja en vez de azul, un pequeño cambio en su plan hubiese ocurrido; y primero pensaría en Alice y después en Bob. El resultado no le preocupa, las listas están pulverizadas después de la doble trituración y cree que ha logrado su objetivo. Lo que ella no sabe, es que Giulia, la líder insurgente, del otro lado del planeta envió la señal luminosa en superposición cuántica de azul y rojo, manipulando en realidad las decisiones de Eileen. Con ello, superpuso dos posibilidades que se desarrollan a la vez. Extrañamente, en el bote de basura donde el último espía dejó los desechos, están las listas intactas. Eileen fracasó ante el poder de la ciencia.
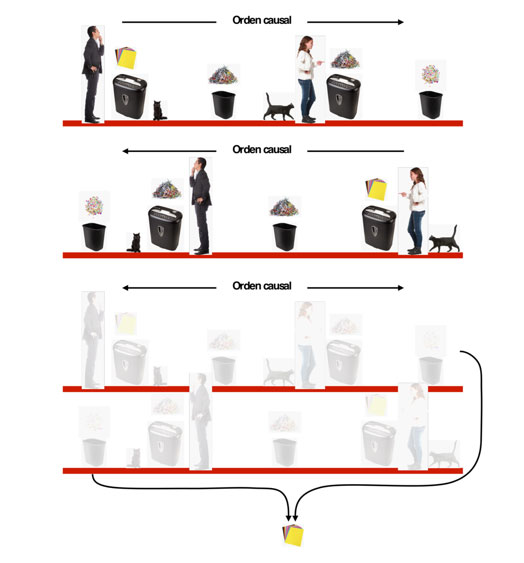
La mecánica cuántica establece que dos eventos o más, físicamente incompatibles, pueden ocurrir simultáneamente en lo que se conoce como una superposición de estados. De esta forma, un sistema que exhiba propiedades cuánticas podría a la vez ocupar dos estados plausibles pero incompatibles entre sí. Por supuesto, cuando dicha propiedad del sistema es medida, sólo uno de los posibles estados emerge en la realidad. Aunque la historia inicial no aparece en el mundo tradicional en que nos desenvolvemos, si existe una versión cuántica de ella. Así, la superposición cuántica nos permite superponer dos interpretaciones del orden en que ocurren los acontecimientos; a este fenómeno se le denomina Orden Causal Indefinido (OCI), el cual explora las ventajas que la superposición cuántica pueda brindar en comunicación y procesamiento cuánticos, dos ámbitos de investigación y desarrollo modernos derivados de la teoría cuántica.
Los fotones -partículas de la luz-, poseen propiedades cuánticas como su energía, polarización, etcétera. Así, un fotón generado por una transición atómica exhibe una energía determinada, pero al pasar por ciertos cristales como borato de bario o niobato de litio (conversión paramétrica descendente, CPD), puede ser absorbido y reemitido como un par de ellos. Los fotones estarán en un estado de superposición de energías, en donde la suma de ambas energías es igual a la del fotón original. Si además, ambas partículas llegan a poseer la misma energía, resultan físicamente indistinguibles. Sin embargo, estos fotones también tienen una propiedad intrínseca llamada polarización, que en el proceso anterior siempre es opuesta, vertical y horizontal, y es lo único que los diferencia. Es decir, en tanto esta propiedad no se mida, no se sabrá cuál de los dos es de qué tipo; más aun, ambos fotones generados por el proceso anterior poseen a la vez ambas características y cada uno es siempre opuesto al otro. A esto se llama entrelazamiento cuántico. Los fotones pueden dirigirse hacia espejos semitransparentes que los filtran en función de su polarización (divisor de haz por polarización, DHP). La reflexión en estos espejos tiene propiedades cuánticas que dependen de la polarización en donde su trayectoria se dirige a cruzar el espejo o ser reflejados, de modo que cada fotón se encuentra en una superposición de trayectorias. Por lo tanto, si ambos fotones se confinan en una trayectoria común, se entenderá que un fotón sigue una trayectoria y el otro, una diferente, debido a sus polarizaciones opuestas, pero no se conocerá cuál va sobre qué trayectoria. De este modo, cada fotón viaja por ambas trayectorias al mismo tiempo en superposición cuántica, pero a la vez, nunca se desplazan ambos por la misma. De otro modo, también es posible provocar que cada fotón vaya por dos caminos diferentes que se bifurcan, dando cuatro trayectorias que sólo surgen simultáneamente por pares.
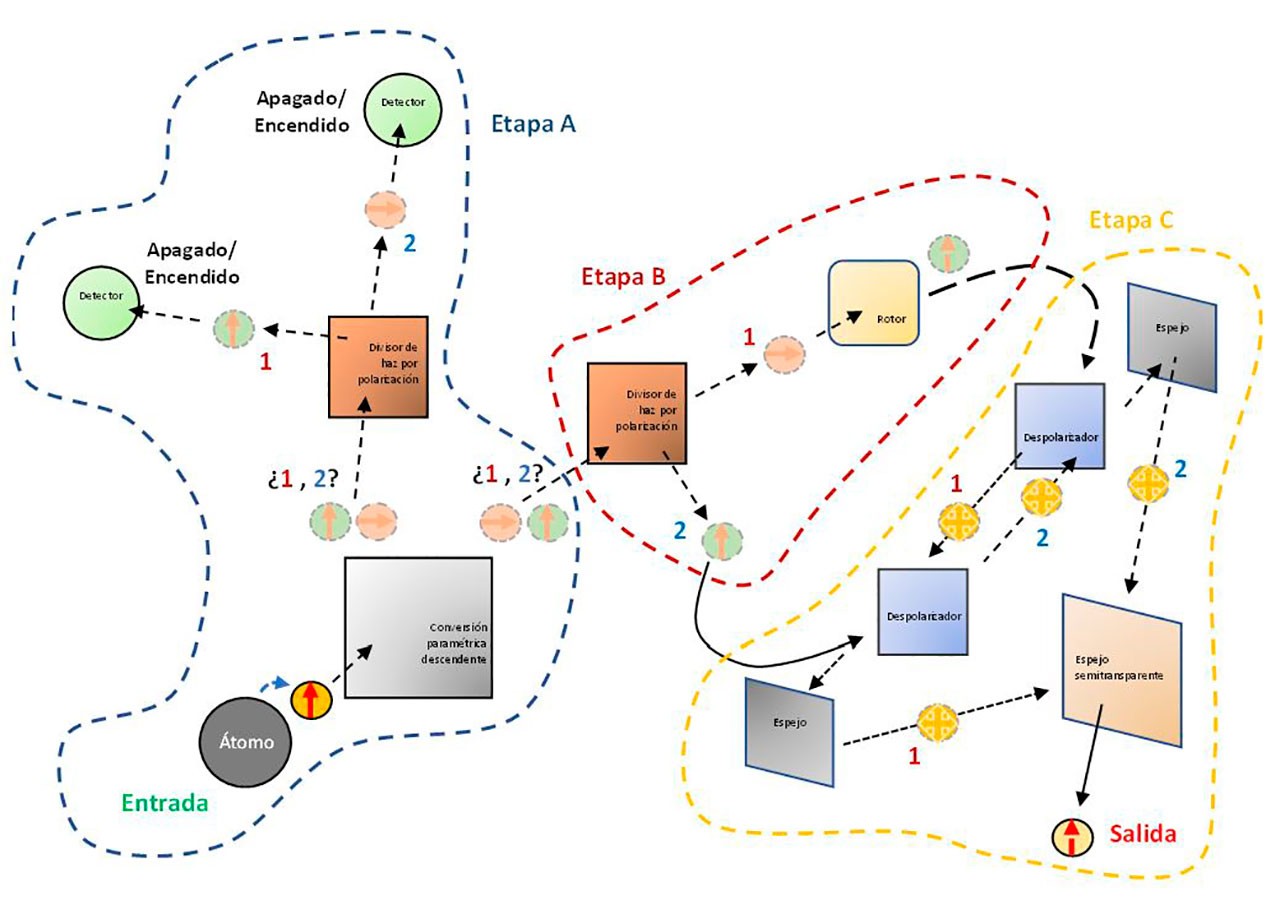
La superposición de estas dos posibilidades sucede naturalmente en los sistemas cuánticos. Estos, además, pueden interactuar con otros, condicionados por sus estados, así que en ellos el mañana se convierte en una superposición de futuros posibles que se bifurca. Puede utilizarse uno de estos sistemas para que, en función de su estado, condicione otras acciones posteriores. En el proceso descrito anteriormente e ilustrado en la parte A de la Figura 2, se añade la etapa B en la cual el fotón del lado derecho que emerge de la CPD (ambas posibilidades, 1 o 2, están presentes, aunque se trata del mismo fotón) se dirige a los dos despolarizadores idénticos (D, cristales que borran toda información de la polarización del fotón incidente) en la etapa C, donde la única diferencia es que recorren su camino en sentido opuesto. Antes de ello, un rotor de polarización (R) modifica la polarización haciéndola idéntica a la de su pareja, de modo que, sobre cualquier trayectoria incidente, el fotón tenga la misma polarización, siendo ahora idénticos salvo por la trayectoria seguida. Al final, las dos trayectorias son recombinadas mediante espejos y un espejo semitransparente (ES), el cual borra la información de la trayectoria por la que el fotón viajó. Con estas condiciones y ajustando la intensidad de la superposición, se puede encontrar al final el fotón incidente intacto con su polarización recuperada, a pesar de que ha pasado en dos ocasiones por el despolarizador que técnicamente borra la información de polarización sobre él. Este es el símil real del archivo intacto en la historia introductoria. Este efecto es el resultado de la interferencia cuántica inducida por el OCI.
Adicionalmente, en la etapa A de la Figura 2 se añadieron dos detectores que no fueron usados hasta ahora. Sorprendentemente si se emplearan para determinar de dónde llega el primer fotón (sólo uno puede detectar al fotón en ese lado de la trayectoria), por lo que la superposición dejaría de existir en ambos lados del montaje y de acuerdo con la mecánica cuántica, el efecto de OCI deja de operar, obteniendo un fotón totalmente despolarizado del lado derecho, el análogo real del archivo destruido en nuestro ejemplo hipotético. Si el fotón intacto recibido del lado derecho en la etapa C no es medido u observado, su estado puede alterarse en cualquier momento posterior si el camino seguido por el fotón del lado izquierdo es determinado por su detección en un proceso denominado post-medición.
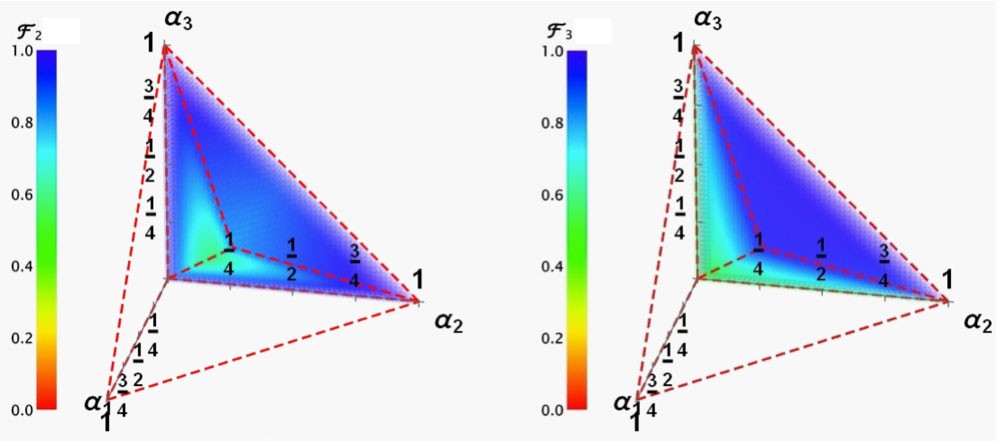
El proceso anterior se ilustra con despolarizadores, ya que fueron los primeros en ser estudiados, aunque resultados similares se han obtenido con otros efectos o canales cuánticos diferentes a los despolarizadores y que incluso no eliminan toda la información del estado entrante. Igualmente puede usarse materia en vez de luz, ya que esto no es una propiedad del sistema empleado, sino de la naturaleza de la mecánica cuántica. Particularmente, se muestra que si el canal es de teleportación cuántica imperfecta, el OCI puede resolver las imperfecciones logrando una teleportación sin errores. Los canales cuánticos de comunicación para qubits que se emplean en aplicaciones de seguridad criptográfica y procesamiento cuántico hoy en día, y llamados canales de Pauli, también son caracterizados con el OCI, observando el mismo fenómeno. La Figura 3 muestra sintéticamente esta singularización en forma paramétrica. El origen de coordenadas corresponde al canal transparente, que secuencialmente o en OCI se mantendrá transparente. Sin embargo, en la cara frontal, los canales con gran pérdida de información que secuencialmente se volverían más imperfectos, se comportan como canales transparentes bajo OCI. Otro aspecto notable es que mientras más órdenes causales se superpongan (aquí se considera el caso de dos), al parecer, se obtienen mejores resultados. Otras aplicaciones plausibles podrían surgir en criptografía cuántica, ya que, por ejemplo, cualquier espía que opere entre ambos despolarizadores, no obtendría información, en tanto que, si no existe espionaje y a ambas superposiciones se les permite arribar a su destino, puede recuperase la información intacta enviada en superposición de orden causal. El proceso podría también frustrarse en caso necesario con un control lejano como la medición por parte de los detectores en el fotón primario.
Hace treinta años, las aplicaciones cuánticas eran sumamente limitadas. En la década actual hay una explosión de ideas que utilizan las propiedades más básicas de la mecánica cuántica en seguridad, comunicación, procesamiento, imagenología, etcétera. Hoy en día, vivimos en una era llena de posibilidades en donde cada vez más profesionales de diversas disciplinas se ven inmersos y atraídos por la mecánica cuántica y sus aplicaciones para relacionarla con la solución de problemas complejos propios de esas áreas, estrechando el carácter multidisciplinario e innovador de la ciencia. Así, con el OCI se ha comenzado a utilizarla para alterar y controlar la causalidad de los acontecimientos de nuestro futuro.
Referencias
Gribbin, J. 1984. En busca del gato de Schrödinger. Biblioteca Científica Salvat: México, México.
Vedral, V. 2011. Descodificando la realidad: el universo como información cuántica. Biblioteca Buridan: Madrid, España.
Kaye, P., Laflamme, R. and Mosca, M. An introduction to quantum computing. Oxford University Press: New York, USA.
Hecht, J. P. Fundamentos de computación cuántica para su aplicación en teoría de la información cuántica y criptografía cuántica. Universidad de Buenos Aires: Buenos Aires, Argentina.
Ebler, D. Salek, S. and Chiribella, G. 2017. Enhanced Communication with the assistance of indefinite causal order, Phys. Rev. Lett. 120, pp. 120502.
Procopio, L.; Delgado, F.; Enríquez, M.; Belabas, N.; and Levenson, J. 2019. Communication enhancement through quantum coherent control of N channels in an indefinite causal-order scenario. Entropy 21 (10), pp. 1012.
Cardoso-Isidoro, C. and Delgado, F. 2020. Symmetries in Teleportation Assisted by N-Channels under Indefinite Causal Order and Post-Measurement. Symmetry 12 (11), pp. 1904.
En memoria del Dr. Bogan Mielnik Manwelow (1936-2019), profesor emérito del departamento de Física del CINVESTAV.











1 comentario
Ah que emperatriz tan loquilla! excelente articulo.
Comentarios no permitidos.