En 1900, los estudios termodinámicos de Max Planck sobre los materiales incandecentes marcaron el punto de partida de la mecánica cuántica, así como la primera revolución cuántica. Esta revolución consistió en el diseño preciso de materiales: emisión luminosa de los materiales involucrados en sistemas de iluminación como los focos; propiedades electrónicas de materiales involucrados en sistemas de cómputo como los semiconductores; entre otros campos de la tecnología. Con el tiempo, la tecnología permitió a la física cuántica la manipulación individual de sistemas microscópicos, en lugar de trabajar con el material macroscópico. En este sentido, la segunda revolución cuántica trata de la manipulación individual de sistemas cuánticos como electrones, moléculas, qubits, entre otros. En este ámbito, el control de los sistemas cuánticos se convierte en un punto central, pues los sistemas cuánticos son fácilmente perturbables por el entorno. Por otro lado, la Revolución Industrial dio lugar a una rama de la ingeniería, llamada Ingeniería de Control, que se basa en el estudio de los modelos matemáticos que describen los fenómenos físicos de los procesos que se desean manipular. Este estudio permite el establecimiento de leyes de control que permiten alcanzar los requerimientos deseados. En la actualidad, se está buscando aplicar la teoría de control para poder manipular sistemas cuánticos como las moléculas.
Si bien es verdad que hay una teoría de control aplicada a sistemas cuánticos, esta labor se ha llevado a cabo mediante las herramientas comunes para los físicos especializados en mecánica cuántica: operador de evolución, espacios de Hilbert, conmutadores, etcétera. No obstante, estas herramientas no son comunes en la comunidad de ingenieros de control. Lo cual ha dificultado que esta comunidad pueda incursionar directamente en esta pujante revolución cuántica. Por este motivo, se ven obligados a seguir cursos y estancias de investigación en mecánica cuántica especializada; lo cual requiere de considerable tiempo y recursos. Por tanto, en el artículo [M. Bonilla-Licea and M. E. Bonilla, “On the Behavioral Reachability of a Confined Molecule Under Laser Action,” in IEEE Transactions on Automatic Control, vol. 69, no. 3, pp. 1689-1696, March 2024, doi: 10.1109/TAC.2023.3326062.], se diseña una metodología que plantea el control de un sistema cuántico en términos familiares para un ingeniero de control: representación de estado, alcanzabilidad del estado, etcétera. Así, se evita el uso de números complejos o la utilización exhaustiva de operadores.
En el artículo se aborda el problema de cambiar el estado oscilatorio de una molécula diatómica en un tiempo finito. Para resolver este problema usando el formalismo de ingeniería de control, se aprovecha que el promedio del momento y la posición intermoleculares, con sus incertidumbres asociadas, siguen ecuaciones dinámicas reales, lineales e invariantes en el tiempo. De esta manera, se forma una representación de estado de estas ecuaciones; es decir, una estructura matemática que permite controlar la dinámica de las variables, sin necesidad de resolver las ecuaciones dinámicas.
Al analizar esta representación de estado (propia de la ingeniería de control), se puede observar, sin resolver ninguna ecuación, que la dinámica de los promedios y las incertidumbres de la molécula están desacoplados. Dicho de otra manera, la situación dinámica de los promedios no afecta a las incertidumbres y viceversa. Más aún, las incertidumbres no son controlables, lo cual significa que no se puede modificar su estado dinámico mediante un agente externo. Esto plantea un cambio de paradigma: Primero hay que asegurarse que la dinámica de las incertidumbres es asintóticamente estable, y luego, diseñar el pulso electromagnético para cambiar el estado oscilatorio de los promedios de la distancia intermolecular, como se muestra en la Figura 1. Este análisis y diseño del pulso electromagnético se lleva a cabo sin la necesidad de resolver ninguna ecuación diferencial, o de manipular exhaustivamente operadores.
Esta nueva metodología propuesta, que se basa en la representación de estado de los promedios e incertidumbres, es una alternativa para los ingenieros de control, puesto que pueden aplicar las metodologías clásicas de control avanzado, sin tener que profundizar en la teoría cuántica.
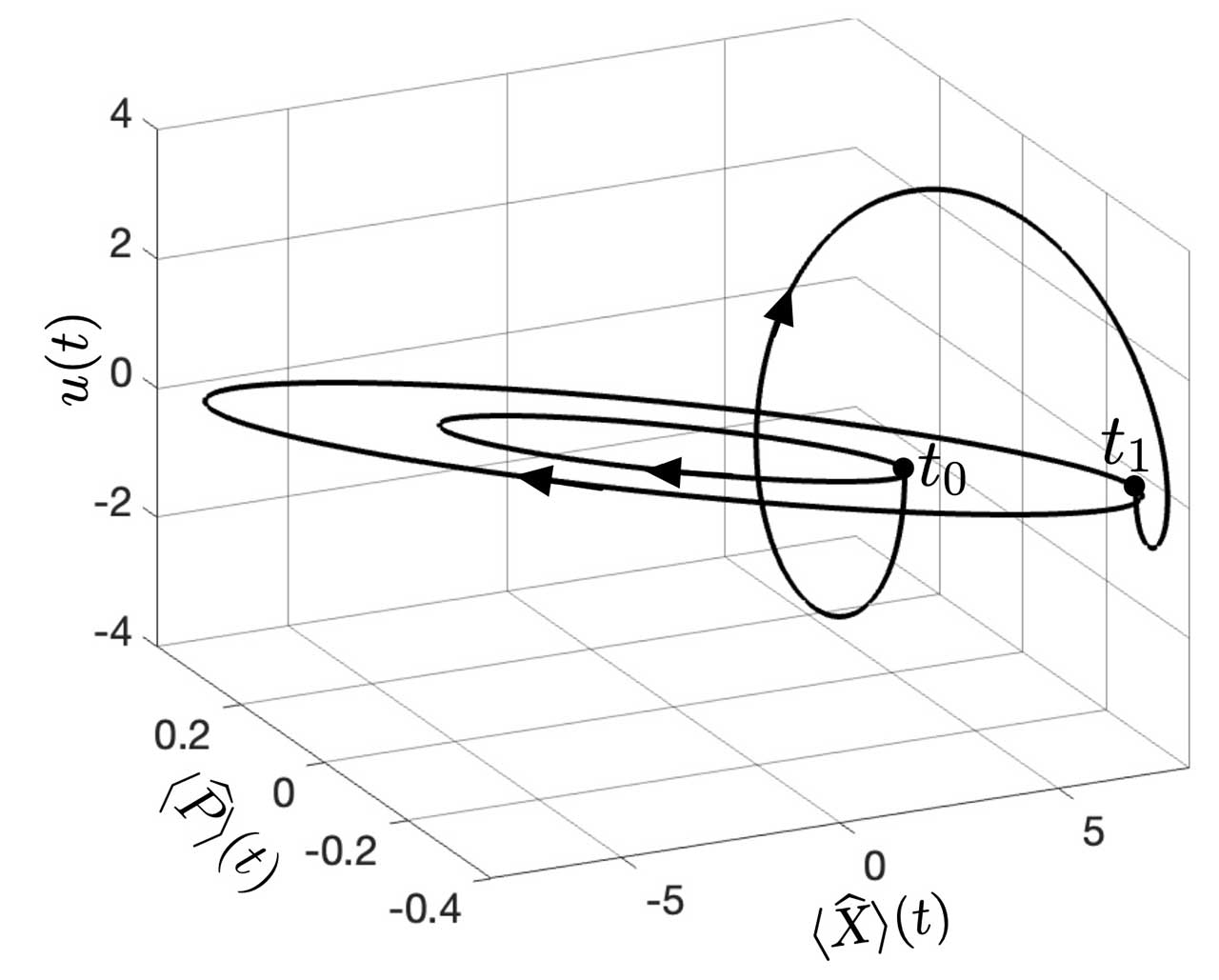Figura 1. Representación gráfica de dos estados oscilatorios elípticos, caracterizados por el momento(t) y la distancia (t) intermoleculares promedios, con la respectiva ley de control u(t).
Referencia
Bonilla-Licea and M. E. Bonilla, “On the Behavioral Reachability of a Confined Molecule Under Laser Action,” in IEEE Transactions on Automatic Control, vol. 69, no. 3, pp. 1689-1696, March 2024, doi: 10.1109/TAC.2023.3326062.
