Resumen: Por mucho tiempo la función exponencial ha jugado un papel fundamental en las matemáticas, y su impacto ha trascendido esta disciplina. En este artículo reseñamos su historia, partiendo desde las civilizaciones antiguas y examinando su evolución en el tiempo. Además resaltamos algunos de los hitos matemáticos que llevaron a la creación de la función exponencial. Finalmente, proporcionamos una mirada breve a cómo la función exponencial es utilizada en áreas como la física, ingeniería y biología.
Cuenta una leyenda que el dios Krishna se presentó ante un rey personificando a un hombre sabio y lo retó a un juego de ajedrez, el juego favorito del rey. Antes de comenzar decidieron lo que sería el premio si ganaba el sabio. Éste dijo que sólo quería una pequeña cantidad de arroz que se calcularía utilizando el tablero de ajedrez. Un grano de arroz se colocaría en el primer cuadro y el número de granos se duplicaría en cada cuadro sucesivo. El rey al perder el juego, se vio obligado a cubrir su deuda. Sin embargo, al ir colocando los granos de arroz en el tablero, pronto se dio cuenta de que no tendría suficiente arroz para pagar. Krishna entonces, se reveló en su verdadera forma y le dijo al rey que podía pagar la deuda poco a poco, ofreciendo arroz gratuito en el templo todos los días hasta que la deuda estuviera completamente pagada.
Esta historia ha sido contada de muchas maneras diferentes con el pasar de los años. En algunas variantes, el personaje del dios Krishna es reemplazado por un siervo, el creador del juego de ajedrez, o un artesano que hace los mejores tableros de juego. En otras versiones se usa trigo en lugar de arroz. También hay variaciones en el final de la historia; en algunas el gobernante mata a la persona que debería recibir el premio, mientras que en otras el premio se da sólo si se cuenta cada grano de manera individual. Sin embargo, el mensaje central de la historia sigue siendo el mismo: el aumento explosivo en un patrón donde cada paso se multiplica por la misma cantidad (progresión geométrica) en lugar de sumársele una cantidad fija (progresión aritmética).
Las raíces de las progresiones geométricas, una forma discreta de la función exponencial, se remontan a la antigua Grecia y posiblemente a los sumerios. Sin embargo, sería hasta el siglo XVIII que, gracias a algunos de los matemáticos más importantes del mundo, la función exponencial fue finalmente descubierta. A pesar de su corta edad, su impacto ha sido enorme y se extiende a muchos campos científicos. Para contar la historia de la función exponencial, es necesario empezar con la invención de los logaritmos.
Los logaritmos fueron creados independientemente por los matemáticos John Napier, de Escocia, y Jost Bürgi, de Suiza, con el objetivo de simplificar los cálculos en la trigonometría esférica, una herramienta utilizada en astronomía y navegación estelar. Aunque Bürgi probablemente creó su sistema de logaritmos alrededor del año 1600, la descripción de Napier fue publicada primero, en 1614, en el libro Mirifici Logarithmorum Canonis Descriptio (Descripción del Maravilloso Canon de Logaritmos), y gracias a ello, fue ampliamente reconocido como el inventor de los logaritmos y tendría gran impacto en su evolución posterior.
Los logaritmos vinculan la multiplicación en los números reales positivos y la suma en los números reales. Napier en particular, definió sus logaritmos como la relación entre dos partículas que se mueven a lo largo de una línea: una con una velocidad constante, y la otra con una velocidad proporcional a la distancia desde un punto fijo. Aunque cumplía con el propósito para el que fue introducido, la definición del logaritmo de Napier, LogNap, era un tanto rebuscada e introducía algunas complejidades innecesarias en los cálculos. Para ilustrar lo anterior, podemos echar un vistazo a la manera en que se relaciona con el logaritmo natural, In:
LogNap(x) = –107In(x/107).
El matemático inglés Henry Briggs hizo dos visitas a Edimburgo en 1616 y 1617 para colaborar con John Napier. Durante sus conversaciones, discutieron y aceptaron la propuesta de Briggs para modificar los logaritmos de Napier. Después de su segunda visita, Briggs publicó en 1617 la primera tabla de sus logaritmos mejorados, conocidos actualmente como logaritmos comunes o base 10 (log10). Su uso se extendió rápidamente debido a la manera en que facilitaban la realización de cálculos complejos. Esto se debió en gran parte a que nuestro sistema de numeración se basa en potencias de 10.
En 1649 Alphonse Antonio de Sarasa, quien fue estudiante de Grégoire de Saint-Vincent, demostró que el área A(t) bajo la hipérbola xy = 1 entre x = 1 y x = t obedece la siguiente relación común a todas las funciones logarítmicas:
A(tu) = A(t) + A(u).
Los matemáticos de la época pronto se dieron cuenta de que esta característica podría llevar a la creación de un nuevo tipo de logaritmo. Así, Mercator publicó en 1668 su libro Logaritmotechnia, con las primeras tablas de lo que ahora se conoce como logaritmo natural.
El libro clásico de Leonhard Euler, Introductio in analysin infinitorum (Introducción al Análisis Infinito), publicado en 1748, marcó el paso final en el desarrollo de logaritmos. Antes de Euler, los logaritmos solían definirse utilizando el cálculo integral. Sin embargo, Euler cambió esto introduciendo la potenciación ax con base a en los números reales positivos, y a partir de esta función definió el logaritmo base a como la función inversa.
El trabajo revolucionario de Jacob Bernoulli en el tema de interés compuesto, abrió el camino para el descubrimiento de la constante que más tarde fue denotada como e por Euler. La contribución de Bernoulli se puede describir de manera concisa de la siguiente manera: considere el crecimiento del capital cuando se invierte a una tasa de interés anual del 100% y se capitaliza en intervalos de tiempo 1/n. Al final del año, el capital se habrá multiplicado por un factor de
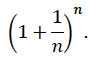
Bernoulli demostró que a medida que aumenta el valor de n, este factor converge a un valor constante entre 2 y 3.
Euler amplió el trabajo de Bernoulli definiendo la función exponencial y el logaritmo natural de la siguiente manera:
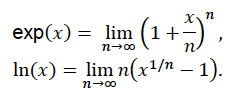
Además, Euler estableció que la función exponencial es una función de potenciación con base e, exp(x) = ex y que la función exponencial y el logaritmo son funciones mutuamente inversas.
En su libro A Mathematician’s Apology, Godfrey H. Hardy argumentó que una idea matemática es seria o significativa si puede conectarse de manera natural y clara con un gran número de otras ideas matemáticas. Así, es altamente probable que un teorema matemático serio, que conecta ideas significativas, conduzca a avances importantes en las matemáticas y en otras ciencias. Hardy utilizó como ejemplo la demostración de Pitágoras sobre la irracionalidad de √2, destacando cómo un teorema simple y elegante puede abrir nuevas vías para el desarrollo de las matemáticas.
La función exponencial es un excelente ejemplo de una idea matemática que ha dejado un impacto duradero, no solo en matemáticas, sino también en otros campos. Se considera una pieza clave para el avance de todas las áreas modernas de matemáticas. Además, sus aplicaciones son diversas y pueden verse en campos como la física, donde explica procesos que van desde el decaimiento radiactivo hasta la dinámica de poblaciones. En finanzas se utiliza en el modelado de tasas de interés y precios de acciones. La función exponencial también es un componente crítico en la ingeniería, donde es fundamental para el desarrollo de circuitos eléctricos, sistemas de control y de comunicación, solo por mencionar algunos ejemplos.
En Introductio in analysin infinitorum Euler introdujo la ecuación que lleva su nombre:
eix = cos x + isin x.
En especial, cuando x = π, esta fórmula conduce a la conocida identidad de Euler:
eix + 1 = 0,
que es considerada por muchos como una de las ecuaciones más hermosas de las matemáticas, ya que combina las tres operaciones matemáticas básicas (suma, multiplicación y potenciación) y relaciona 5 constantes matemáticas fundamentales (0, la identidad aditiva; 1, la identidad multiplicativa; la unidad de los números imaginarios, i, π y e). La identidad de Euler es un punto de convergencia de diversas disciplinas matemáticas, como la aritmética, la trigonometría y la teoría de números complejos.
La fórmula de Euler también ha sido de gran importancia en la física y la ingeniería a través, entre otros ejemplos, del análisis de Fourier, el cual permite descomponer funciones complejas en sumas de funciones trigonométricas simples y cuyas aplicaciones más significativas incluyen:
- Procesamiento de señales: en el análisis y manipulación de señales como las de audio, imágenes y voz.
- Compresión de imágenes: en algoritmos de compresión de imágenes para reducir la cantidad de datos necesarios para representar una imagen.
- Análisis espectral: en el estudio de los componentes de frecuencia de las señales, como las producidas por objetos vibratorios u ondas electromagnéticas.
- Diseño de filtros: en la creación de filtros electrónicos que eliminen frecuencias no deseadas de las señales.
- Transferencia de calor: en el análisis del flujo de calor en sólidos y fluidos.
- Mecánica cuántica: en el estudio del comportamiento de partículas en un estado cuántico.
- Sismología: en el análisis de la propagación de ondas sísmicas.
- Análisis electromagnético: en el estudio del comportamiento de campos electromagnéticos.
- Análisis de señales neuronales: en el estudio de los campos eléctricos y magnéticos emanados de la actividad cerebral.
- Análisis de la estructura de proteínas: para determinar la estructura de las proteínas mediante cristalografía de rayos X.
En conclusión, la función exponencial ha trascendido el ámbito de la teoría matemática y se ha convertido en una herramienta vital en diferentes campos. Su impacto ha sido inconmensurable en el desarrollo de las ciencias naturales y sociales y ha permanecido como una fuerza impulsora detrás de numerosos avances tecnológicos.
Los lectores interesados en una comprensión más profunda de la historia de las funciones exponenciales y logarítmicas encontrarán interesante la serie de artículos History of the Exponential and Logarithmic Concepts, publicados en 1913 en la American Mathematical Monthly, volumen 20, números 1 a 7. Estos artículos pueden ser consultados de forma gratuita en Jstor en la siguiente URL: https://www.jstor.org/.