Constantes universales
Los cambios de temperatura en Monterrey, Nuevo León, son de locura. Hace justo dos meses tuvimos una temperatura de – 6 ºC; dentro de unos días, según el pronóstico del tiempo, tendremos 40 ºC. Tales inclemencias climáticas, que son tan naturales en esta parte del país –se dice que en Nuevo León el clima es muy estable porque siempre está fatal–, me hicieron recordar el pendiente de escribir este ensayo. Mi propósito, que fui postergando por casi dos años, me vino después de leer la noticia, en mayo de 2019, que la Conferencia General de Pesos y Medidas (CGPM, por sus siglas en francés) aprobó en noviembre de 2018 una nueva definición del kelvin, la unidad de la escala absoluta de la temperatura. No tenía prisa por escribir estas líneas, después de todo la definición aprobada en la CGPM es la definitiva, ya que se da en términos de una constante universal, la llamada constante de Boltzmann. Tuvieron que pasar veinticuatro siglos desde Empédocles de Agrigento – primer griego en preguntarse qué era el frío y el calor– para llegar a esta definición.
La temperatura la sentimos en carne propia, así que en todos estos siglos hemos tratado de abstraer tal sensación corporal y medirla de forma objetiva. Se podría afirmar que la historia de la temperatura devela la lucha del ser humano para domeñar su subjetividad en aras del conocimiento objetivo.
La definición del kelvin y otras unidades físicas era una asignatura pendiente que los metrólogos del mundo tenían desde hace mucho tiempo. Sabían que algún día la humanidad tenía que realizar mediciones en términos de unidades basadas en constantes universales. ¿Cómo era posible que nosotros lo terrícolas midiéramos el tiempo, la masa, la longitud, la temperatura, etcétera, con las varas de lo terrenal y mundano? Una civilización extraterrestre avanzada se hubiera desternillado de risa al descubrir que la masa de un objeto dado, por ejemplo un asteroide, se midiera al compararla con un cilindro de platino e iridio resguardado en una vitrina en el pabellón de Sevres, a las afueras de París; o que la distancia entre el Sol y la Tierra se midiera usando como unidad de longitud una barra guardada también en ese pabellón. Ahora podemos dormir tranquilos, todas las variables físicas que usamos en la vida diaria tienen ya unidades decorosas en términos de constantes universales que aquí, en China o en algún exoplaneta de otro sistema solar, habrán de conocer. Pues si en otra civilización lejana no conocen, por ejemplo, qué es la constante de Planck – con la que ahora se mide la masa– o la constante de Boltzmann, peor para ellos. Querrá decir que su conocimiento científico aún no es tan elevado como el nuestro.
Así que el 20 de mayo de 2019, la definición del kelvin en términos de la constante de Boltzmann (KB), entró en vigor. Ahora, cuando usemos la escala absoluta ya no pensaremos en un grado como una fracción de la temperatura del punto triple del agua (de hecho, el inverso de ella: 1/273.16), la habremos de medir en términos de KB.

¿Qué es, o cómo surge, la constante de Boltzmann? La respuesta no es nada sencilla, pues las vicisitudes para llegar a ella fueron tantas que al final contribuyeron a la muerte de quien la propuso; quitándose la vida por alguna razón desconocida, pero seguramente agravada porque los científicos contemporáneos se mofaban de sus ideas. El mejor valor conocido al día de hoy de la constante de Boltzmann es el siguiente: 1.380649 X 10-23 J/K (la J es la abreviación de joules, unidades de energía). La nueva definición “cobra” sentido dado que la energía (E) está relacionada con la temperatura (T) de la siguiente manera: E = KBT. Así, es claro que un grado kelvin equivale a 1.380649 X 10-23 J.
Las cosas se aclaran si pensamos en la escala de temperatura a la que estamos acostumbrados: la escala Celsius (o grados centígrados). Sabemos desde la primaria que el agua se congela a cero grados centígrados; lo que quizás es menos conocido es que en la escala kelvin el agua se congela a 273.16 K. También sabemos que el agua hierve (al nivel del mar) a 100 grados centígrados; en kelvin son 373.16 K. Para no ir más lejos: la temperatura debajo de nuestra lengua es 37 ºC, o bien 310.16 K. Un dato más: el cero absoluto en kelvin, aquella temperatura en la que el único movimiento remanente de la materia es cuántico, equivale a -273.16 ºC.
Palos de ciego
La percepción que sentimos en la piel en un invierno crudo, que nos hace cubrirnos con una prenda afelpada para no tiritar de frío, o aquella que nos agobia en un intenso día de calor y que nos impulsa a desvestirnos, nos da sin duda la sensación de temperatura. “Hoy amaneció muy frío”; “hoy hace un calor infernal”; “parece que traes fiebre”; “se me antoja una cerveza helada”. Estas frases son ahora normales y usadas por toda la gente, pero imaginemos hace cientos de años cuando el ser humano quiso entender qué era esa sensación externa a su cuerpo que lo hacía cubrirse o descubrirse. Uno de los primeros en pensar en si se podía cuantificar el frío o calor fue Empédocles de Agrigento, cinco siglos antes de nuestra era. Y dos milenios después, llegó Galileo con su invento del primer termómetro, un instrumento que le permitía medir, en una graduación dada, la suya propia, el desplazamiento de una columna de agua producido por la expansión, o contracción, del aire retenido en el instrumento.
Luego vinieron ingeniosos intentos para crear una escala de temperatura que fuera aceptada por la mayoría. Rømer (1644-1710) propuso que el cero de su escala fuera el punto de congelación de una salmuera y el punto de ebullición del agua tuviera el valor de 60. Entonces dividía ese intervalo entre 60, para que cada división fuera un grado. Isaac Newton no quiso quedarse atrás y propuso una escala en que el cero fuera el punto de congelación del agua y 12 la temperatura del cuerpo humano. A saber en qué estaba pensando el físico alquimista.
Poco tiempo después, Daniel Fahrenheit (1686-1736) dio un paso más allá: estableció el cero de su escala como el punto de congelación de una salmuera concentrada y la temperatura del cuerpo humano como 96 ºF. En su escala, el agua pura se congelaba a 32 ºF y bullía a 212 ºF. A Fahrenheit también se le ocurrió sustituir el agua o vino por mercurio, que es utilizado hasta la fecha. La puja por las escalas prosiguió: Rene Antoine Ferchault de Réamur puso el cero en el punto de congelación del agua y el de ebullición en 80, mientras que Joseph-Nicolas Delisle le dio la contra: el cero cuando el agua bullía y 150 cuando se congelaba.
Parecían palos de ciego. Nadie sabía qué era la temperatura, pero había que quedarse con el premio (un termómetro universal). En el penúltimo intento, el astrónomo sueco Andrés Celsius propuso que el cero fuera asociado al punto de ebullición del agua y el 100 a su congelación. No estaba mal la idea, las dos fases del agua estaban a cien grados una de otra, así que era una escala más fácil de usar. Aunque con los números al revés. Después de su muerte, algún juicioso decidió intercambiarlos: 0 para la congelación y 100 para la ebullición. Y ésta es la escala utilizada en casi todos los hogares del mundo, a excepción de los de un puñado de países lunáticos que siguen usando la escala Fahrenheit, entre los que destaca el que más recursos dedica a la ciencia, Estados Unidos.
Todas estas escalas estaban basadas en la comparación con eventos térmicos conocidos: la congelación del agua, su ebullición, la temperatura corporal, etcétera. Así que son escalas relativas ligadas a substancias. Los termómetros eran entonces dispositivos que registraban lo empírico. ¿No había una escala absoluta que no dependiera de lo que le ocurriera a una substancia?
No era una pregunta ociosa. Guillaume Amontons (1663-1705) justo se hizo en 1702 la pregunta: ¿cuál era la temperatura más baja que podría existir en la naturaleza? En su mente, quizá, no pensaba en alguna substancia, sólo en el hecho de si un frío infinito podía existir.

La escala absoluta
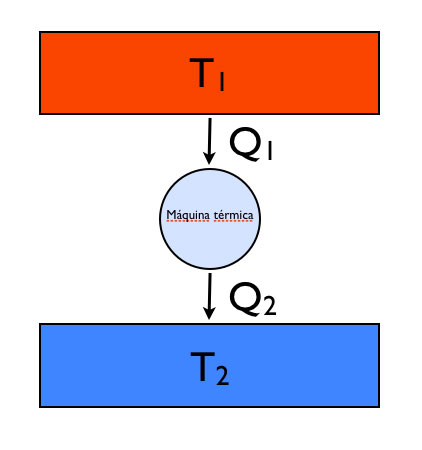
En 1848 y 1854 William Thomson, profesor de la Universidad de Glasgow, publicó dos trabajos que establecieron que para que una escala absoluta pudiera existir, se requería una teoría que no dependiera de substancia alguna [1]. Tal conexión entre abstracción y empirismo era el colofón de la termometría que por siglos se había desarrollado. Propuso que si a un cuerpo se le podría extraer calor y enfriar de una temperatura T (en su escala absoluta) a una temperatura T-1, llegaría el punto en que no se podría enfriar más. Se habría entonces llegado al cero absoluto, o frío infinito. No podía existir en el universo, en esta nueva escala, una temperatura más baja que cero. Con esta propuesta se conectaba por primera vez el calor con la temperatura. Tal concepto se conoció después como la Primera Temperatura Absoluta. Seis años después, tomando en cuenta el trabajo de Carnot y Joule sobre una máquina térmica que opera recibiendo un calor Q1 del reservorio térmico que se encuentra a una temperatura T1, y que luego entrega un calor Q2 a otro reservorio que está a una temperatura T2 (ver imagen), Thomson dedujo la siguiente expresión: T1/T2 = Q1/Q2.
La eficiencia de esta máquina es 1 – Q2/Q1 (si Q2 = 0, la máquina es ideal y tiene eficiencia 1; si Q2 = Q1 , la máquina no produce ningún trabajo y su eficiencia es cero). El mérito de Thomson fue haber visualizado que la eficiencia podía ser expresada también como 1 – T2/T1, por lo que T1/T2 = Q1/Q2. Con esta ecuación se concebía una segunda forma, más robusta, de la temperatura absoluta, ya que si T1 = 0 entonces Q1 = 0. El cero absoluto existía (no es posible extraer calor de un reservorio que se encuentra a una temperatura cero). Esta nueva definición se llamó la Segunda temperatura absoluta [1].

Muy cerca del laboratorio donde Thomson trabajaba fluía lentamente el meandro de un río llamado Kelvin. Cuando al padre de la escala absoluta la Reina Victoria le otorgó el título de Barón, éste se convirtió en Lord Kelvin. Así, la escala absoluta de la temperatura se la debemos a Thomson, el nombre de las unidades al río.
¿Pero qué es la temperatura? Si bien Lord Kelvin concibió una escala para todas las temperaturas de la naturaleza, desde el cero absoluto (0 K) hasta la temperatura más elevada que haya existido jamás: 1.42 x 1032 K (10-44 segundos después del Big Bang), no dejó dicho qué cosa era eso que medía y estaba relacionado con el calor. Hoy en día tenemos termómetros de todo tipo que usamos para medir temperatura; inalámbricos, de mercurio, de platino, de estado sólido; tenemos al menos tres escalas para medirla: la Fahrenheit, la Celsius y la absoluta cuyos grados son los kelvin, pero tal parece que no sabemos qué es lo que medimos.
Un cuerpo tiene masa, que podemos medir en kilogramos (usando la constante de Planck), y sabemos qué es: es ese algo que el planeta atrae (masa gravitacional) o bien ese algo que nos cuesta mover (masa inercial). Podemos empujar con nuestro cuerpo un carrito de golf porque tiene poca masa (inercial), no podemos empujar un tráiler porque tiene mucha. Podemos cargar una pelota de boliche (poca masa gravitacional), pero no podemos hacerlo con una casa porque tiene mucha. Un cuerpo tiene volumen, longitud al cubo, y sabemos qué es: es ese algo que ocupa un lugar en el espacio: más volumen, más lugar. Una pelota de futbol tiene más volumen que una de tenis. Un metro es la distancia que avanzamos si damos un paso largo; diez kilómetros (diez mil pasos largos) es lo que debemos caminar al día si queremos mantenernos en forma.
Máquina de Carnot
¿Pero la temperatura? ¿Qué es? Si ponemos bajo nuestra lengua un termómetro de mercurio marcará 37 ºC; si marca más, tenemos fiebre. Cuanto más se dilate el mercurio dentro del termómetro y veamos que la columna color plata sube, más fiebre tenemos. ¿Pero por qué nuestra temperatura corporal dilata la columna de mercurio? ¿Qué relación hay entre el interior de nuestra lengua y el metal líquido mercurio? Desde luego, la transmisión de calor entre ambos.
Antes de continuar, me arriesgo a afirmar que algo se les pasó a los inventores de la temperatura. Ésta es una variable intensiva, a diferencia, por ejemplo, del volumen que es extensiva. Si queremos saber el volumen total de nuestra casa lo que podemos hacer es medir el volumen de cada espacio (las recámaras, los baños, la cocina, etcétera) y luego hacer la suma. Sin embargo, si queremos saber su temperatura, no sumamos las temperaturas de cada cuarto; las medimos con un termómetro y luego calculamos el promedio. Podemos pensar entonces que la temperatura es una variable rara, imprecisa, de “segunda clase”; porque al estar asociada a un promedio de entrada no podemos conocerla bien. Este hecho debió darle una idea a Thomson: si la temperatura era una variable intensiva, entonces de entrada era un promedio de algo. Pero no lo vio.
En 1859, y luego con más profundidad en 1866, James Clerk Maxwell dio un paso gigantesco para resolver el enigma [2]. Publicó dos artículos trascendentales que sacudieron la termodinámica en la que William Thomson había fincado su teoría sobre la escala absoluta de la temperatura. Los artículos de Maxwell teorizaban sobre la distribución de velocidades de los átomos y/o moléculas en gases. Los átomos y moléculas no se habían visto aún, pero empezaba a consolidarse la idea de que la materia estaba compuesta por ellos. Otros pensadores anteriores a Maxwell ya habían externado ideas similares. El filósofo romano Lucrecio (50 a.C.) consideraba que estos corpúsculos ultramundanos se movían en todas las direcciones en el aire; Daniel Bernoulli (1738) propuso que la presión de un gas sobre una superficie (como nuestra piel) era causada por el golpeteo de tales átomos; August Krönig (1856) y al año siguiente Rudolf Clausius (1857) elaboraron teorías cinéticas para describir el movimiento atómico que componían los gases. Pero Maxwell sugirió que las velocidades de los componentes de un gas seguían una distribución estadística, en la que había un despliegue continuo de velocidades, no una sola [3].
El promedio de tal distribución se relacionaba con la temperatura. Ésta dejaba de ser una variable misteriosa, que requería un termómetro para medirla, y pasaba a ser una energía cinética promedio, cuyas unidades se medían en joules. El logro de Thomson fue relacionar la temperatura con el calor; el logro de Maxwell fue establecer que éste era energía cinética. Así, el cero absoluto era ausencia de energía cinética.
Regresando al ejemplo de la temperatura corporal que nos medimos con un termómetro de mercurio: lo que ocurre es que entre la boca y éste, se transfiere energía cinética. Los átomos y moléculas de nuestra lengua golpetean a los átomos del vidrio, y éstos a su vez golpetean a los del mercurio, que se alejan entre ellos por la agitación y por ende la columna se dilata. No conocemos exactamente la energía de los golpeteos atómicos, por eso calculamos el promedio.
¿Por qué se siguieron usando los kelvin para medir la temperatura, por qué no se decidió cambiar a joules, las unidades de energía? La razón todos la conocemos, aunque nunca pensamos en ello: el ser humano es un ser conservador. Cuando algo funciona bien, mejor dejarlo como está. Además hay intereses, títulos nobiliarios, hechos históricos. No por ser científicos dejamos de ser humanos, con todos los atributos que ya sabemos se nos dan bien.
Pero vayámonos con tiento, que el tema es controversial. Pensando sobre la máquina de Carnot, Clausius definió una función de estado, que llamó entropía, como el calor Q dividido entre la temperatura T (Q/T). Para desmenuzar esta expresión, que parece sencilla pero da muchos dolores de cabeza, hagamos un experimento mental: elévese una bola de billar a un metro (100 cm) de altura del piso de su casa; déjela caer. Rebotará, pero jamás llegará a la altura original. En el mejor de los casos llegará a 90 cm del piso. ¿Por qué? ¿Hay algo que se pierde? Sí y no, depende de cómo se vea. El principio de conservación de energía, que dice que ésta no se crea ni se destruye, que sólo se transforma, nos salva la plana: la energía potencial de la bola de billar antes de soltarla es igual a la que recupera después del rebote más la que se roba el universo (10%). Y esa energía que el universo se lleva, es calor que ya no se puede usar para nada. Es la moneda de cambio por existir, lo que nos cobra el universo por permitirnos habitarlo. Pasa a ser una energía inútil, inservible. No la podemos usar, por ejemplo, para elevar diez centímetros a otra bola similar. Esa energía que aparentemente desaparece es calor en el aire por donde pasó la bola en su caída, en el piso donde rebotó, en la bola al abollarse. Adiós energía cinética.
Clausius nos enseñó que este desperdicio de energía se relacionaba con ese algo que llamó entropía y estaba dada por Q/T. En otras palabras, en la era pre-atómica de Clausius sólo se sabía que al realizar un trabajo mecánico se generaba calor, que no podía ser usado para realizar otro tipo de trabajo y eso se relacionaba con la entropía.
¿Qué habría ocurrido si después del descubrimiento de Maxwell se hubiera medido la temperatura en joules? Lo de menos es que tal vez no se le hubiera dado el título de Barón a Thomson, aunque tampoco a Maxwell, porque a pesar de que lo merecía más, era escocés. Muchas cosas, que no podemos explicar en este corto ensayo, habrían pasado, pero hay una que es obvia, la entropía no tendría unidades [4]. En efecto, al ser la división de dos energías (Q/T), las unidades se cancelarían. Una entropía sin unidades hubiera hecho las cosas más sencillas. Para empezar, Boltzmann no hubiera tenido tantos problemas con los físicos de la época que lo desdeñaban (como Ernst Mach, Loschmidt, Poincaré), pues en su definición estadística de la entropía no habría tenido necesidad de usar ninguna constante (en lugar de expresarla como S = K log Ω, donde Ω es el número de estados accesibles del sistema, simplemente sería: S = log Ω). Observe el lector que en la expresión de S, he usado K, no KB. Fue Max Planck quien bautizó la constante utilizada por Boltzmann (K = nR; donde n es número de moles y R la constante universal de los gases ideales), como constante de Boltzmann.
Si S es una medida de disipación de energía, ¿tendría significado que tal disipación fuera adimensional? Claro que sí. Hoy la usaríamos como Claude Shannon la propuso en 1948 en un artículo sobre la teoría matemática de la información [5]: la entropía, sin unidades, es una medida de ignorancia. Entre menor sea, nuestro conocimiento sobre el sistema será mayor. Un ejemplo muy simple sería lanzar una moneda, en lugar de un dado, para hacer una apuesta. En el primer caso la entropía es menor.
Cuentan que John von Neumann le recomendó a Shannon usar el término de entropía al discutir sobre información, ya que en un debate siempre tendría la ventaja porque nadie sabe qué es la entropía [6].
En un sistema físico, ¿a qué ignorancia se podría referir S? Desde luego a la ignorancia del calor, pues en una máquina térmica que disipa calor, éste es una energía que no sabemos cómo se difumina en el universo; cómo mueve las moléculas del aire o los átomos en una superficie, cómo se pierde para siempre sin retorno. Entre más calor disipe un sistema físico, mayor es nuestra ignorancia o entropía. Si nos preguntamos qué ocurre con el calor que se genera al estrellar un martillo contra una pared, es como si quisiéramos saber cuántos átomos saldrán disparados a una velocidad de mil metros por segundo, cuántos a cien metros por segundo, etcétera. Habrá toda una distribución de velocidades que no podemos conocer.
La ignorancia, dicho sea como colofón, es una de las fuentes de nuestro conservadurismo. No nos aventuramos a cambiar nada porque no sabemos qué nos depara el destino. El aventurero, como el sol, es un ente de baja entropía. Pero todos, o casi todos, preferimos vivir con mucha. Inventamos el concepto de temperatura absoluta de la mano del concepto de entropía, y cosa curiosa, ésta última nos intimidó en el intento de hacer más sencilla a la primera. Entropía e ignorancia, ignorancia y entropía. Así va la civilización humana dando tumbos en la ciencia y en la vida.
Jesús Carlos Ruiz Suárez, Cinvestav-Unidad Monterrey
Referencias
[1] Hasok Chang, Inventing Temperature: Measurement and Scientific Progress, OXFORD UNIVERSITY PRESS (2004). [2] W. D. Niven, The Scientific Papers of James Clerk Maxwell, Vol. Two, Dover Publications, Inc. (2003). [3] La idea de una distribución estadística para representar fenómenos físicos le vino a Maxwell en 1857, al trabajar sobre los enigmáticos anillos de Saturno. La composición de tamaños de éstos, ahora sabemos, sigue la distribución de Maxwell: desde granitos de polvo hasta rocas de decenas de metros. Sólo un genio es capaz de pasar de un fenómeno (granular) a otro (termodinámico). [4] Arieh Ben-Naim, Entropy Demystified, World Scientific, Singapore 596224 (2008). [5] C. E. Shannon, “A mathematical theory of communication,” in The Bell System Technical Journal, vol. 27, no. 3, pp. 379-423, July 1948, doi: 10.1002/j.1538-7305.1948.tb01338 [6] M. Tribus and E. C. McIrvine, Energy and Information, Scientific American, 225, 179-188 (1971).