Pasaporte al aprendizaje: Cursos de matemáticas en línea para bachillerato

Introducción

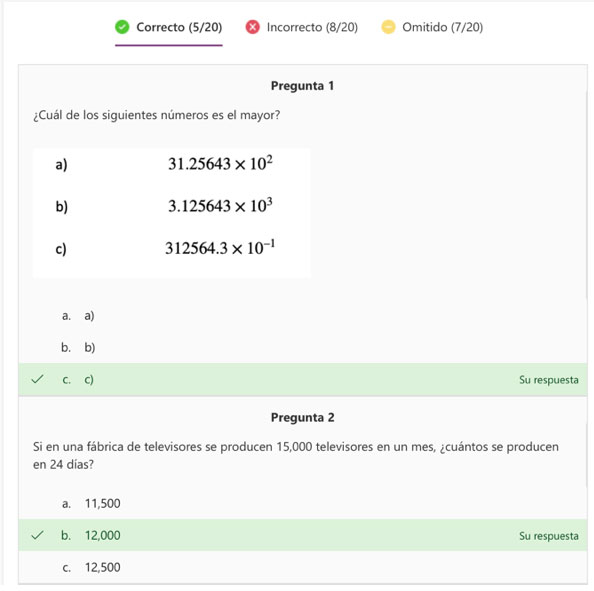
El confinamiento social impuesto como medida para controlar la propagación de la pandemia COVID-19, ha generado cambios y ajustes importantes en los ambientes de aprendizaje en todas las disciplinas alrededor del mundo. Los escenarios híbridos que combinan el trabajo remoto y las clases presenciales apuntan hacia un nuevo modelo para estructurar y promover el desarrollo y construcción del conocimiento disciplinario de los estudiantes.

En términos generales, el contrato didáctico que implícitamente sustentaba las responsabilidades y tareas de maestros y estudiantes en ambientes presenciales, requiere o demanda cambios y ajustes asociados con la naturaleza y funcionamiento de un ambiente mixto de aprendizaje. En este escenario, el estudiante extiende sus tareas y responsabilidades relacionadas con la consulta y discusión de contenidos en línea que complementa y amplía la información sobre los temas estudiados durante las clases presenciales.

En el proceso de comprender conceptos o formular y solucionar problemas, los alumnos pueden consultar recursos y plataformas disponibles en línea donde expertos en el tema expliquen temas del curso o analicen problemas resueltos. Así, la tarea va más allá de que los jóvenes repitan explicaciones o apliquen reglas para resolver ejercicios; resalta la actividad de contraste y análisis de las diferentes formas de representar conceptos y discutir su aplicación en el estudio de otros temas o situaciones.

En la parte presencial, más que escuchar la presentación de su profesor, los alumnos tienen la oportunidad de mostrar y compartir sus avances e ideas sobre el tema en estudio, plantear sus dudas, conocer y analizar los acercamientos de sus pares y recibir retroalimentación directa del maestro. En este camino, se enfatiza que los jóvenes centren su formación en los procesos de formular y responder preguntas como un medio para expresar y discutir sus ideas, y para la comprensión de conceptos y resolución de problemas.

¿Cómo diseñar y estructurar un ambiente de aprendizaje que considere actividades presenciales y remotas? ¿Cómo aprenden los estudiantes en un escenario que les exige trabajar y realizar actividades en línea y también participar en discusiones presenciales? ¿Cómo monitorear y evaluar el aprendizaje de los estudiantes? ¿Qué ajustes son necesarios realizar en las propuestas del currículum? ¿Qué tecnologías digitales son importantes en el diseño y desarrollo de un ambiente híbrido de enseñanza? ¿Qué ajustes necesita la infraestructura del ambiente presencial para promover la participación continua y segura de los estudiantes? Éstas son algunas interrogantes en la agenda académica de la Educación Matemática y son parte de diversos programas de investigación que buscan sustentar un escenario combinado de aprendizaje.

En este contexto, los materiales que guían a los estudiantes son un factor importante para el desarrollo y construcción del pensamiento disciplinario. La idea es que, durante el estudio del contenido de los cursos, los alumnos tengan la oportunidad de revisar y extender la comprensión de los conceptos y gradualmente robustecer y ampliar sus acercamientos de resolución de problemas. Aquí, resulta importante que los jóvenes desarrollen e instrumenten plan táctico y estratégico que los oriente en la selección y estudio de contenidos que aparecen en línea o en plataformas digitales.

Algunos recursos disponibles en línea pueden contribuir en el desarrollo de las experiencias de aprendizaje de los estudiantes en términos de revisar materiales o explicaciones sobre conceptos matemáticos o ejemplos resueltos.

El uso de aplicaciones digitales, como GeoGebra, amplían las formas de representación, exploración y análisis de conceptos o relaciones matemáticas para los diferentes casos. En este camino, es importante que los estudiantes usen diversas tecnologías y desarrollos o plataformas digitales durante las fases de comprensión de los enunciados, el diseño de un plan de solución y en comunicación y discusión de los resultados y extensiones del dominio inicial de las tareas.

Además, con el uso de algunas aplicaciones (Zoom, Teams, Google Meet, etcétera.) pueden compartir y discutir sus ideas con sus pares y analizar y contrastar las diversas formas de solución de distintos temas.

¿Cómo diseñar y transformar los cursos tradicionales de matemáticas que se estudian en la educación preuniversitaria en un modelo que incorpore el uso sistemático de tecnologías digitales? A continuación, se esbozan elementos esenciales que soportan el desarrollo de los temas que se abordan en los cursos de matemáticas de bachillerato. Estos son parte de un proyecto (Pasaporte al Aprendizaje) que el Cinvestav y UNICEF coordinan para este nivel.

En Pasaporte al Aprendizaje, una estrategia didáctica que guía y sustenta el desarrollo de los contenidos, incluye la presentación de problemas resueltos donde se ilustra lo que significa y se espera de los estudiantes al resolver tareas o comprender un concepto. Por ejemplo, se fomenta la idea de que los estudiantes, al enfrentar un problema, siempre busquen y discutan diferentes maneras de resolverlo.

En este camino, deben analizar y discutir con sus pares las estrategias y recursos importantes involucrados en proceso de resolverlos. Las aplicaciones digitales de comunicación permiten a los estudiantes compartir sus ideas y discutir con sus compañeros y maestros sus preguntas, comentarios, dudas y acercamientos de resolución de problemas. Posteriormente, los estudiantes trabajarán algunos problemas siguiendo y respondiendo las preguntas que los guían hacia su resolución, y finalmente resuelven tareas de manera independiente. Los cursos aparecen en una plataforma que los estudiantes activan a través de un registro y código. De manera general, la estructura de los cursos se organiza alrededor de cuatro módulos de contenidos que incluyen los siguientes apartados:

a. Presentación (video corto) donde se explica cómo trabajar las actividades del curso y un cuestionario inicial, con preguntas de opción múltiple que informa sobre el dominio de los estudiantes sobre conceptos y recursos, previamente estudiados. Al terminar el cuestionario, los estudiantes conocerán qué preguntas respondieron correctamente y sugerencias sobre cómo revisar los contenidos involucrados en las preguntas que no respondieron adecuadamente.

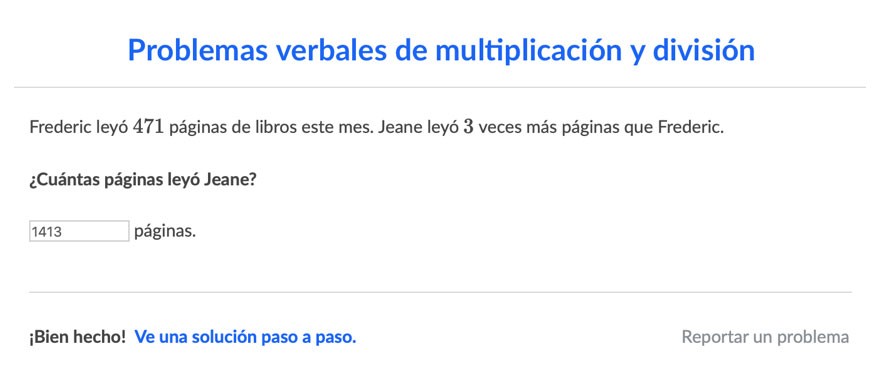
b. Ejemplos de problemas resueltos donde se muestra a los estudiantes diversos métodos sobre cómo resolverlos. Se identifican conceptos, estrategias y recursos asociados con diversos métodos de solución. En este proceso se plantean preguntas que los estudiantes responderán durante las fases de comprensión, exploración y resolución de las tareas. Además, al final se presenta un cuestionario que extiende y generaliza la aplicación de los métodos de solución a otras familias de problemas.

c. Enlaces de plataformas en línea que los estudiantes consultan con la intención de revisar y ampliar la comprensión de conceptos relacionados con el tema.

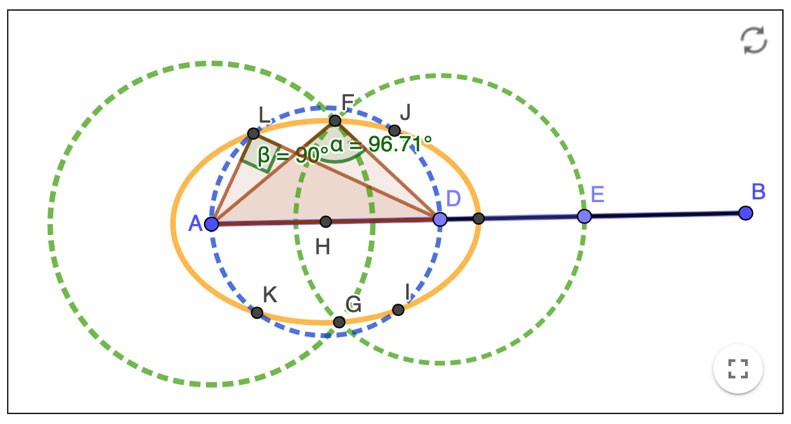
d. Construcción y exploración de modelos dinámicos. Aquí se usa la aplicación “GeoGebra” para construir y explorar modelos geométricos de las tareas. Por ejemplo, en el estudio de las secciones cónicas, en el curso de Geometría Analítica, se construyen modelos dinámicos que privilegian el acercamiento geométrico que permite construir referentes asociados con las propiedades de las cónicas. Por ejemplo, si se tiene el perímetro de un triángulo rectángulo y el valor de su hipotenusa. ¿Cómo se puede construir ese triángulo? El modelo vinculado a esta pregunta que involucra la construcción de una familia de triángulos con un lado la longitud de la hipotenusa (AD) y los otros lados AF y DF tienen longitudes DE & EB respectivamente, siendo AB la longitud de perímetro. El lugar geométrico de los puntos G & F cuando el punto D se mueve sobre el segmento AB genera la elipse. Por construcción la suma de los lados AF & DF es una constante (definición de elipse). En este acercamiento se enfatiza el significado geométrico de los objetos matemáticos y posteriormente se estudia el modelo algebraico de las cónicas.

e. Problemas propuestos que los estudiantes tienen que resolver y que amplían el horizonte de aplicación de los conceptos estudiados.

f. Un sistema en línea de asesorías para los estudiantes. Un maestro supervisa el trabajo de los estudiantes y responderá las preguntas y dudas que hacen llegar los alumnos a través de un “chat” o un mensaje por correo electrónico.

De manera general, en el desarrollo de los cursos se integra el uso de tecnologías y desarrollos digitales como videos cortos, cuestionarios sobre el dominio de los contenidos (autoevaluación); ejemplos y actividades resueltas, ligas o enlaces sobre temas relacionados; construcción y exploración de modelos dinámicos y una evaluación global sobre el desempeño de los estudiantes.

El grupo de trabajo que coordino y participa en el diseño y desarrollo de los contenidos de los cursos incluye egresados del departamento de Matemática Educativa del Cinvestav (Adrián Gómez Arciga, Daniel Ortiz May, y Miguel Cerón Villegas). La parte técnica que contempla la integración y activación de la plataforma digital está coordinada por Luis A. Ortiz Arellano.