En noviembre de 2018, la prestigiada revista IEEE Transactions on Computers, publicó una edición especial dedicada a presentar los avances más novedosos en la sub-disciplina conocida como criptografía post-cuántica. El título de dicha edición especial fue: “Special Issue on Cryptographic Engineering in a Post-Quantum World: State of the Art Advances”.
En esta reseña se explican brevemente las principales contribuciones científicas reportadas en el artículo de Faz-Hernández, López, Ochoa-Jiménez y Rodríguez-Henríquez titulado: “A Faster software implementation of the Supersingular Isogeny Diffie-Hellman Key Exchange Protocol”, el cual fuera publicado en la edición especial arriba mencionada. Cabe destacar que Faz-Hernández y Ochoa- Jiménez estudiaron su maestría en Ciencias en el Departamento de Computación. Actualmente, Ochoa- Jiménez está por terminar su doctorado en Ciencias en el Departamento de Computación. Un dato interesante es que las iniciales de los co-autores forman la palabra “FLOR”, razón por lo cual el trabajo descrito aquí, adoptó el logotipo mostrado en la figura 1. Por simplicidad, en lo que resta de esta reseña, nos referiremos al grupo de co-autores como equipo FLOR.

En 1976, en el artículo parteaguas: “New directions in cryptography”, se presentó por primera vez el protocolo Diffie-Hellman. Este procedimiento permite establecer de manera segura una llave secreta entre dos partes, las cuales por hipótesis, están restringidas a intercambios de mensajes en un canal de transmisión inseguro. El protocolo Diffie-Hellman fue el primer procedimiento que hizo uso del paradigma de criptografía de llave pública, propulsando una verdadera revolución en la disciplina. Esta revolución permitió el desarrollo de aplicaciones masivas y de uso cotidiano de seguridad informática en los dominios de comercio, banca y gobierno electrónicos, por mencionar sólo algunos de los más relevantes.
En el paradigma de criptografía de llave pública o asimétrica, existen dos llaves distintas: una para cifrar y otra para descifrar. La llave para cifrar es conocida públicamente y, por ende, se denomina llave pública. La llave para descifrar sólo es conocida por el receptor del mensaje, por lo que se le denomina llave privada. Una ventaja de estos sistemas criptográficos es que la denominada llave pública puede ser usada por cualquier persona para cifrar mensajes bajo la premisa de que sólo quien posea la llave privada podrá descifrar dichos mensajes. Aunque los métodos de llave pública son muy poderosos, tienden a tener un costo computacional elevado.
La seguridad de los criptosistemas de clave pública clásicos que están en uso hoy en día, descansa en la complejidad computacional de resolver un problema matemático asociado a cada uno de estos esquemas. Algunos ejemplos de dichos problemas matemáticos son: La factorización de números enteros gigantes, el cómputo de logaritmos discretos también de números gigantes, etc. Se cree, sin que exista una certidumbre absoluta, que estos problemas son extremadamente difíciles de resolver cuando se utilizan métodos convencionales, pues los mejores algoritmos para atacarlos observan una complejidad computacional sub-exponencial.
Por otro lado, a principios de los años ochentas del siglo pasado una serie de científicos entre los que destacan Paul Benioff, Yuri Manin y Richard Feynman, propusieron el concepto de cómputo cuántico. Aunque han pasado ya 38 años desde la propuesta inicial de este insólito paradigma, el estado de la tecnología de las computadoras cuánticas está aún en sus fases iniciales. Sin embargo, en los últimos años se han logrado resultados espectaculares, los cuales permiten alimentar la esperanza de que a mediano plazo será posible construir un ordenador cuántico con capacidades de cómputo superiores a los dispositivos clásicos disponibles hoy en día.
Dentro de las posibles aplicaciones que han sido sugeridas para computadoras cuánticas, probablemente la más llamativa de todas sea la propuesta en los años noventas por el afamado investigador Peter Shor. En 1992, Peter Shor presentó un algoritmo que de ser ejecutado en una computadora cuántica poderosa, permitiría resolver el Problema de Factorización Entera (PFE) en un tiempo con complejidad polinomial al tamaño del número entero analizado. Para propósitos prácticos, ello significa que desde el punto de vista computacional, el PFE se vuelve un problema “fácil”. En contrapartida, el PFE es todavía considerado un problema computacionalmente difícil cuando se intenta atacarlo por medio de computadoras convencionales (clásicas). Más aún, utilizando variantes del algoritmo de Shor sería también posible resolver con “facilidad” el problema del logaritmo discreto. Ello implicaría que la seguridad informática ofrecida por aplicaciones masivas de uso cotidiano en los dominios de e-gobierno, e-comercio, transacciones bancarias electrónicas, etc, se volverían vulnerables, como quien dice, de la noche a la mañana.
Sin embargo, desde el bando de los criptógrafos no todo está perdido, pues el algoritmo de Shor no permite romper todos los esquemas convencionales de criptografía de llave pública existentes. Aunque debido a su alta complejidad computacional, los esquemas que se le resisten al algoritmo de Shor no suelen utilizarse en aplicaciones comerciales, la amenaza de una inminente llegada de computadoras cuánticas de alta capacidad ha motivado una revisión profunda de todos estos esquemas. Esta revisión ha dado nacimiento a una nueva sub-disciplina conocida como criptografía post-cuántica.
De manera general, se define como sistemas criptográficos post-cuánticos a los esquemas clásicos para los cuales el algoritmo de Shor no se puede aplicar de manera efectiva. Hasta el momento uno de los candidatos más prometedores, es el protocolo de intercambio de llaves Diffie-Hellman utilizando curvas elípticas supersingulares isógenas (SIDH por sus siglas en inglés). Este esquema fue propuesto en 2011 por los investigadores de la Universidad de Waterloo, David Jao y Luca de Feo (este último hacía una estancia post-doctoral en dicha Universidad).
Utilizando conjeturas matemáticas muy bien establecidas, se considera que la variante SIDH del protocolo Diffie-Hellman, sí podría resistir todos los ataques cuánticos conocidos hasta el momento. A pesar de estas sólidas garantías de seguridad, el protocolo SIDH es relativamente lento comparado con esquemas post-cuánticos que han sido propuestos utilizando otros problemas matemáticos difíciles. Esta situación ha obligado a que desde que el protocolo SIDH fuera propuesto, hubiese un enorme interés por encontrar técnicas algorítmicas y/o matemáticas más eficientes para la implementación de dicho procedimiento.
En el artículo escrito por el equipo FLOR, se reportan mejoras algorítmicas que permiten optimizar la ejecución del protocolo SIDH por un factor de aceleración de 1.33 comparado con la implementación más rápida reportada hasta antes de dicho trabajo. Las principales mejoras algorítmicas presentadas en este artículo recaen principalmente en un cuidadoso estudio de la operación de multiplicación escalar en curvas elípticas utilizando el procedimiento conocido como la escalera de Montgomery.
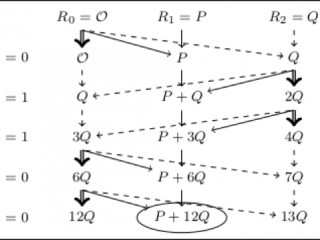
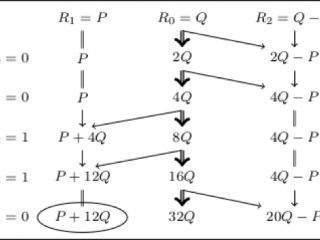
En efecto, cuando Jao y de Feo propusieron el protocolo SIDH consideraron que el cómputo de cada peldaño de su escalera de Montgomery tendría un costo de dos sumas y un doblado de punto. Sin embargo, el equipo FLOR mostró que cada peldaño puede calcularse utilizando únicamente una suma y un doblado de punto. Esta ingeniosa observación permite obtener grandes ahorros en el cómputo del protocolo SIDH, pero a cambio obliga a reestructurar cuidadosamente varias primitivas básicas de dicho procedimiento. Estas modificaciones son discutidas en detalle en el artículo reseñado e ilustradas para un ejemplo de juguete en la siguiente figura, en la cual se describe cómo realizar el cálculo de la operación P + 12Q, donde P y Q son puntos que pertenecen a una curva elíptica supersingular E definida sobre el campo finito GF(p²), donde p es un número primo de 751 bits.
Puede decirse entonces que el artículo “A Faster software implementation of the Supersingular Isogeny Diffie-Hellman Key Exchange Protocol”, desarrollado en su mayor parte por el equipo FLOR en el Departamento de Computación CINVESTAV, constituye un paso hacia adelante en la adopción del protocolo SIDH como la versión más segura para hacer un intercambio de llaves entre dos partes que se enfrentan a un adversario capaz de lanzar ataques cuánticos de gran escala en contra de ellos.