Imagen del autor. Consulte artículo original.
El desarrollo o construcción de conocimiento disciplinar depende directamente de los artefactos o herramientas disponibles que un individuo o grupo activa en los procesos de comprensión o desarrollo de conceptos y en el planteamiento y resolución de problemas.
Las tabletas de arcilla usadas por los Babilonios (1830-1531 a. C.) registran problemas, métodos, y resultados matemáticos en áreas como la aritmética, la geometría y resolución de ecuaciones. Herramientas como la regla y el compás inspiraron construcciones asociadas con el desarrollo de la geometría griega. Euclides (325-265 a.C.) introduce el método axiomático que privilegia el rigor y la demostración en matemáticas. Descartes (1596-1650) inventa el sistema cartesiano que origina un acercamiento algebraico al estudio de la geometría (la geometría analítica).
En términos generales, los artefactos o herramientas pueden ser objetos materiales, como la regla y el compás, un objeto abstracto como el sistema cartesiano o un algoritmo para resolver una ecuación cuadrática, o una aplicación digital como GeoGebra que ofrece un conjunto de herramientas para representar, explorar y resolver problemas matemáticos.
Cuando los individuos usan o activan las funcionalidades de la herramienta exhiben un proceso de apropiación de sus potencialidades que los lleva a transformarla en un instrumento de resolución de problemas. Esta apropiación implica que el individuo desarrolle esquemas cognitivos que norman el uso de ese instrumento durante el proceso de resolución. Es decir, el sujeto construye un medio para resolver un tipo de tareas y éste incluye los componentes del artefacto para afrontar la tarea y los esquemas cognitivos que le permiten realizar el cometido y controlar la actividad.
En este contexto, nos interesa analizar y documentar cómo el uso coordinado de herramientas digitales como los Sistemas de Geometría Dinámica (GeoGebra) inciden tanto en el desarrollo de conocimiento matemático como en las formas de aprender esos contenidos y su aplicación en la resolución de problemas. En particular, una herramienta como GeoGebra ofrece funcionalidades que permiten construir modelos dinámicos de problemas matemáticos y ofrece caminos para explorar el comportamiento de familias de objetos y sus propiedades.
En nuestro programa y agenda de investigación se destaca el uso de tecnologías digitales en la reconstrucción de teoremas y relaciones matemáticas que se estudian en la educación preuniversitaria. Específicamente, nos interesa caracterizar las formas de razonamiento matemático que el individuo puede construir o desarrollar a partir del uso sistemático y coordinado de tecnologías y desarrollos digitales en la solución de interrogantes.
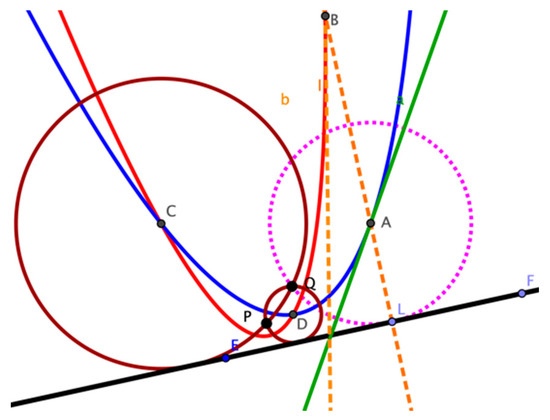
Recientemente, junto con dos colegas de nuestro grupo, publicamos un artículo que muestra la importancia del uso de desarrollos en línea (Wikipedia) en la tarea de contextualizar y situar históricamente los temas involucrados en los enunciados de los problemas. En este caso, se discute el problema de Apolonio que trata de la construcción de circunferencias tangentes a tres circunferencias dadas.
Además, con el uso de GeoGebra se potencia y extiende el uso de estrategias como la exploración de casos más simples y el relajamiento de condiciones iniciales del problema. En esta dirección, se destaca la aplicación de estrategias asociadas con el uso propio de la herramienta como el movimiento controlado de los objetos, la medición de los atributos, el trazo de lugares geométricos de ciertos objetos y la generación de resultados parciales que apuntan a una forma dinámica de explorar y resolver el problema. En este proceso, las secciones cónicas como la parábola y la hipérbola surgen durante la exploración de casos particulares del problema y generan relaciones importantes para resolverlo.
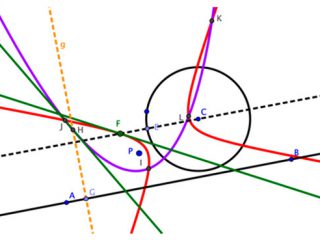
En el artículo se traza una estrategia didáctica para introducir el uso de tecnologías digitales en la resolución de problemas matemáticos.
Referencias
- Santos-Trigo, M. (2020) Problem-solving in mathematics education. InEncyclopedia of Mathematics Education, 2nd ed.; Lerman, S.E., Ed.; Springer: Cham, Switzerland, 2020; pp. 686–693. [Google Scholar] [CrossRef]
- Santos-Trigo,M.; Barrera-Mora, F.; Camacho-Machín, M. (2021). Teachers’ Use of Technology Affordances to Contextualize and Dynamically Enrich and Extend Mathematical Problem-Solving Strategies. Mathematics, 9, 793. https://doi.org/10.3390/math9080793
