Un Covering Array (CA) es un diseño combinatorio que es expresado como una matriz de N renglones por k columnas. Cada renglón representa un experimento de un proceso particular y cada columna representa una variable de dicho proceso.
El contenido de una celda en el renglón “i” y columna “j”, indica el valor que toma la variable “j” en el experimento “i”. La principal restricción que satisface un Covering Array es que en cada sumbmatriz de tamaño N por t columnas aparece al menos una vez cada uno de los posibles valores de las “t” columnas.
La principal dificultad de construir CAs óptimos está en diseñarlos con el menor número de renglones (menor valor de N). En este artículo (https://doi.org/10.1016/j.ins.2018.10.048 ) se presenta un enfoque basado en grafos para construir CAs.
El algoritmo que definimos para construir CAs es denominado GBGA (Greedy Based Graph Algorithm). Nuestro enfoque requiere encontrar una biyección entre una matriz (correspondiente a un CA) y un grafo.
Un grafo G=(V,E) está descrito por un conjunto V de nodos y un conjunto E de arcos.
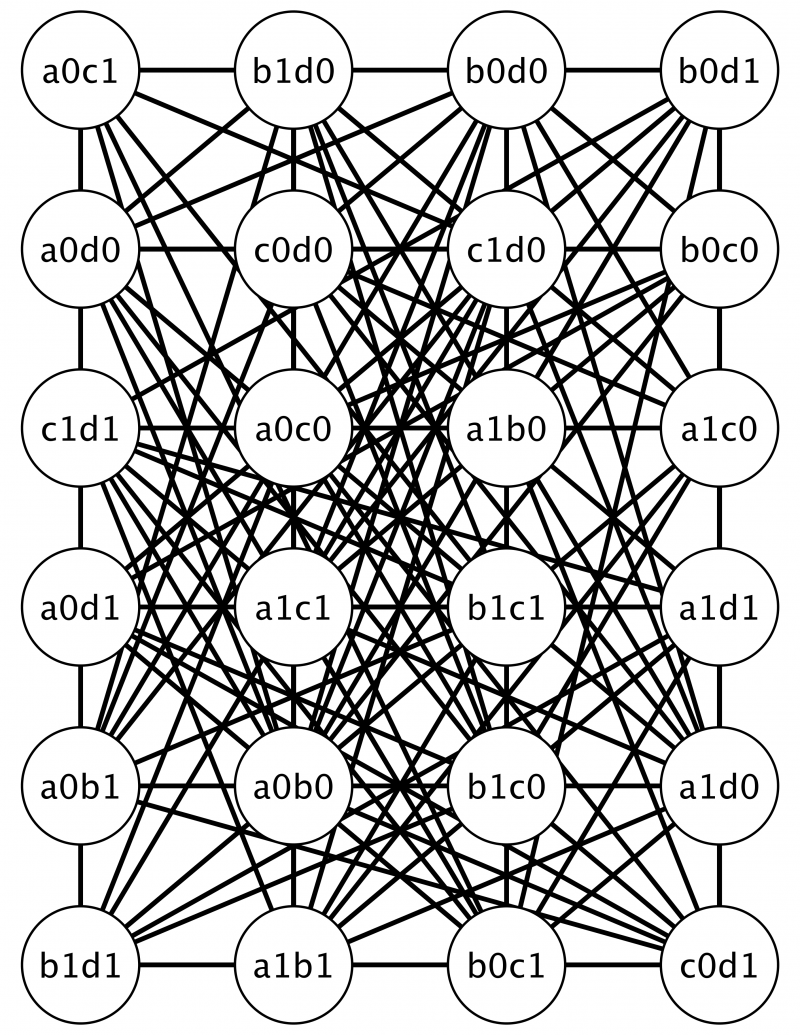
En nuestra representación cada vértice o nodo equivale a una combinación de tamaño “t” de los valores que deben cubrir “t” columnas del CA, y existe un arco entre cada par de nodos sí y sólo sí ambos nodos son compatibles. Esto quiere decir que las columnas en común de los dos nodos, tienen el mismo valor.
En este contexto, el equivalente a un renglón de un CA es un subconjunto de mayor tamaño de nodos que son compatibles por parejas (a este subconjunto de mayor cardinalidad se le denomina MaxClique).
Entonces, la construcción de un CA en el dominio de grafos implica encontrar un subconjunto de mínima cardinalidad de MaxCliques, esto es, el CA tendrá el menor número de renglones.
GBGA usa una estrategia voraz para construir cada uno de los MaxCliques y de acuerdo a los resultados obtenidos con nuestro enfoque, se puede concluir que constituye una buena alternativa para construir CAs.
José Torres Jiménez y José Carlos Pérez Torres
CINVESTAV, Tamaulipas